Abstract
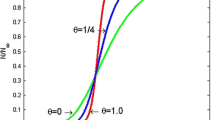
To analyze growth curve quantitatively theu-w diagram is proposed. Herew is defined as any growth quantity at a given time of observation andu is defined as the ratio of relative growth rate ofw tow. Theu-w diagram can be obtained by plotting a series of observed values ofu andw on log-log coordinates.
Theu-w relationship constructed to lead a generalized form of the logistic and Mitscherlich curve results in the growth curve almost equivalent to the curve expected from the Bertalanffy differential equation and thus includes the Richards growth function as a special case. These results show that the approach using theu-w diagram appears to give a useful tool for the growth analysis in general and to be flexible.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Bertalanffy, L. von. 1949. Problems of organic growth. Nature163: 156–158.
Causton, D.R. andJ.C. Venus. 1981. The Biometry of Plant Growth. Edward Arnold, London.
Nishiwaki, Y. andK. Shinozaki. 1952. A new method of representing the population growth. J. Osaka City Med. Center1: 150–156 (in Japanese).
Oberhettinger, F. 1970. Hypergeometric functions.In: M. Abramowitz and I.A. Stegun, ed., Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables p. 555–565. Dover Publications, New York.
Osumi, S. andY. Ishikawa. 1983. Applicability of the Richards' growth function to analysis of growth of tree. Sci. Rep. Kyoto Pref. Univ. Agr. No.35: 49–76 (in Japanese with English summary).
Richards, F.J. 1959. A flexible growth function for empirical use. J. Exp. Bot.10: 290–300.
Shidei, T. ed. 1963. Productivity of forest ecosystem in terms of cycling of matter. Material1: 104 (in Japanese).
Shinozaki, K. 1962. Logistic theory of plant growth. D. Sc. thesis, Kyoto Univ. (in Japanese).
— 1976. Effects of removal on a growing system. Physiol. Ecol. Jap.17: 101–107 (in Japanese with English summary).
— andT. Kira. 1961. TheC-D rule, its theory and practical uses. J. Biol. Osaka City Univ.12: 69–82.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Hozumi, K. Phase diagrammatic approach to the analysis of growth curve using theu-w diagram —Basic aspects. Bot Mag Tokyo 98, 239–250 (1985). https://doi.org/10.1007/BF02488774
Received:
Issue Date:
DOI: https://doi.org/10.1007/BF02488774