Skip to main content
SpringerLink
Log in

An asymptotic-numerical analysis for the lower bound dynamic buckling estimates

  • Published:
Acta Mechanica Sinica Aims and scope Submit manuscript

Abstract

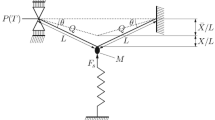
A finite element asymptotic analysis for determining the lower bound dynamic buckling estimates of imperfection-sensitive structures under step load of infinite duration is presented. The lower bound dynamic buckling loads and the corresponding displacements are sought in the form of asymptotic expansions based on the static stability criterion and they can be determined by solving numerically (FEM) several linear problems with a single nonsingular sub-stiffness matrix.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Budiansky B, Roth RS. Axisymmetric dynamic buckling of clamped shallow spherical shells. Collected Papers on Instability of Shell Structures, NASA TN D-1510, 1962

  2. Kounadis AN. Nonlinear dynamic buckling of discrete dissipative or nondissipative systems under step loading.AIAA J, 1991, 29(2): 280–289

    Article  Google Scholar 

  3. Kounadis AN, Mallis J, Raftoyiannis J. Dynamic buckling estimates for discrete systems under step loading.ZAMM, 1991, 71(10): 391–402

    MATH  Google Scholar 

  4. Kounadis AN. Nonlinear dynamic buckling and stability of autonomous structural systems.Int J Mechanical Sciences, 1993, 35(8): 643–656

    Article  MATH  Google Scholar 

  5. Gantes C, Kounadis AN. Energy-based dynamic buckling estimates for autonomous dissipative systems.AIAA J, 1995, 33(7): 1342–1349

    MATH  Google Scholar 

  6. Simitses GJ. Dynamic Stability of Suddenly Loaded Structures. Berlin: Springer-Verlag, 1990

    MATH  Google Scholar 

  7. Wu B. A method for determining the lower bound dynamic buckling loads of imperfection-sensitive structures.ZAMM, 1997, 77: in press

  8. Budiansky B. Theory of buckling and post-buckling behaviour of elastic structures.Advances in Applied Mechanics, 1974, 14: 1–65

    Google Scholar 

  9. Ikeda K, Murota K. Critical initial imperfection of structures.Int J Solids and Structures, 1990, 26(8): 865–886

    Article  MATH  Google Scholar 

  10. Riks E, Brogan FA, Rankin CC. Numerical aspects of shell stability analysis. in: Krätzig WB, Oñate E eds. Computational Mechanics of Nonlinear Response of Shells. Berlin: Springer-Verlag, 1990. 125–151

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Jilin University, 130023, Changchun, China

    Wu Baisheng

Authors
  1. Wu Baisheng
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

The project supported by the State Education Commission of China

Rights and permissions

Reprints and permissions

About this article

Cite this article

Baisheng, W. An asymptotic-numerical analysis for the lower bound dynamic buckling estimates. Acta Mech Sinica 13, 165–170 (1997). https://doi.org/10.1007/BF02487923

Download citation

  • Received:

  • Revised:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF02487923

Key Words

Search

Navigation