Abstract
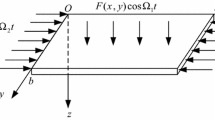
The global bifurcations and chaos of a simply supported rectangular thin plate with parametric excitation are analyzed. The formulas of the thin plate are derived by von Karman type equation and Galerkin's approach. The method of multiple scales is used to obtain the averaged equations. Based on the averaged equations, the theory of the normal form is used to give the explicit expressions of the normal form associated with a double zero and a pair of pure imaginary eigenvalues by Maple program. On the basis of the normal form, a global bifurcation analysis of the parametrically excited rectangular thin plate is given by the global perturbation method developed by Kovacic and Wiggins. The chaotic motion of thin plate is also found by numerical simulation.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Holmes P J. Center manifolds, normal forms and bifurcations of vector fields with application to coupling between periodic and steady motions.Physica D, 1981, 2: 449–481
Yang X L, Sethna P R. Local and global bifurcations in parametrically excited vibrations nearly square plates.Int J Non-linear Mech, 1990, 26: 199–220
Feng Z C, Sethna P R. Global bifurcations in the motion of parametrically excited thin plate.Nonlinear Dynamics, 1993, 4: 389–408
Kovacic G, Wiggins S. Orbits homoclinic to resonance with an application to chaos in a model of the forced and damped sine-Gordon equation.Physica D, 1992, 57: 185–225
Tian W M, Namachchivaya N S, Malhotra N. Non-linear dynamics of a shallow arch under periodic excitation-II. 1∶1 internal resonance.Int J Non-linear Mech, 1994, 29: 367–386
Abe A, Kobayashi Y, Yamada G. Two-mode response of simply supported, rectangular laminated plates.Int J Non-linear Mech, 1998, 33: 675–690
Malhotra N, Namachchivaya N S. Chaotic dynamics of shallow arch structures under 1∶2 internal resonance conditions.Journal of Engineering Mechanics, ASCE, 1997, 123: 612–619
Malhotra N, Namachchivaya N S. Chaotic dynamics of shallow arch structures under 1∶1 internal resonance.Journal of Engineering Mechanics, ASCE, 1997, 123: 620–627
Chia C Y. Non-linear Analysis of Plate. New York: McGraw-Hill, 1980
Nayfeh A H, Mook D T. Nonlinear Oscillations. New York: Wiley-Interscience, 1979
Yu P, Zhang W, Bi Q S. Vibration analysis on a thin plate with the aid of computation of normal forms.Int J Non-linear Mech, 2001, 36: 597–627
Wiggins S. Global Bifurcations and Chaos-Analytical Methods. New York: Springer-Verlag, 1988
Feng Z C, Wiggins S. On the existence of chaos in a parametrically forced mechanical systems with broken O(2) symmetry.Z Angew Math Phys (ZAMP), 1993, 44: 201–248
Nusse H E, Yorke J A. Dynamics: Numerical Explorations. New York: Springer-Verlag, 1997
Author information
Authors and Affiliations
Additional information
The project supported by the National Natural Science Foundation of China (10072004) and by the Natural Science Foundation of Beijing (3992004)
Rights and permissions
About this article
Cite this article
Wei, Z. Analysis of global dynamics in a parametrically excited thin plate. Acta Mech Sinica 17, 71–85 (2001). https://doi.org/10.1007/BF02487771
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF02487771