Abstract
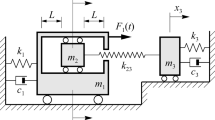
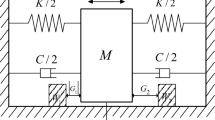
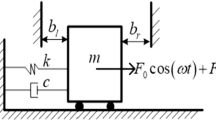
The coexisting periodic impacting motions and their multiplicity of a kind of dual component systems under harmonic excitation are analytically derived. The stability condition of a periodic impacting motion is given by analyzing the propagation of small, arbitrary perturbation from that motion. In numerical simulations, the periodic impacting motions are classified according to the system states before and after an impact. The numerical results show that there exist many types of vibro-impacts and the bifurcation of periodic vibro-impacts is not smooth.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Shaw SW, Holmes PJ. A periodically forced piecewise linear oscillator.Journal of Sound and Vibration, 1983, 90(1): 129–155
Hu HY. Advances in dynamics of piecewise-smooth mechanical systems.Journal of Vibration Engineering, 1995, 8(2): 331–341
Sung CK, Yu WS. Dynamics of a harmonically excited impact damper: bifurcations and chaotic motion.Journal of Sound and Vibration, 1992, 158(2): 317–329
Cusumano JP, Bai BY. Period-infinity periodic motions, chaos, and spatial coherence, in a 10 degree of freedom impact oscillator.Chaos, Solitons & Fractals, 1993, 3(5): 515–535
Author information
Authors and Affiliations
Additional information
Project supported in part by National Natural Science Foundation of China under the grant 59572024 and in part by Trans-century Training Program Foundation for the Talents by the State Education Commission of China
Rights and permissions
About this article
Cite this article
Dongping, J., Haiyan, H. Periodic vibro-impacts and their stability of a dual component system. Acta Mech Sinica 13, 366–376 (1997). https://doi.org/10.1007/BF02487196
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF02487196