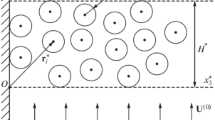
Abstract
The shape of the free surface of a layer of granular material moving on an inclined plane is studied on the basis of a model of a non-Newtonian fluid with a nonlinear relation between the stress tensor and the shear rate of the flow. For small but finite elevations of the free surface, the governing equations are reduced to a quasilinear Burgers equation. Results of a numerical solution are presented for the case of arbitrary elevations.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
K. Hutter and K. R. Rajagopal, “On flows of granular materials,”Continuum Mech. Thermodyn.,6, 81–139 (1994).
R. A. Bagnold, “Experiments on a gravity free dispersion of large solid spheres in a Newtonian fluid under shear,”Proc. Roy. Soc. London,A225, 49–63 (1954).
K. Hutter, “Time-dependent surface elevation of an ice slope,”J. Glaciology,25, No. 92, 247–266 (1980).
V. E. Nakoryakov, B. G. Pokusaev, and I. R. Shreiber,Propagation of Waves in Gas- and Vapor-Liquid Media [in Russian], Inst. Thermal. Phys., Sib. Div., Acad. of Sci. of the USSR, Novosibirsk (1983).
Yu. A. Berezin,Modeling Nonlinear Wave Processes, VNU Sci. Press, Utrecht (1987).
Additional information
Institute of Theoretical and Applied Mechanics, Siberian Division, Russian Academy of Sciences, Novosibirsk 630090. Translated from Prikladnaya Mekhanika i Tekhnicheskaya Fizika, Vol. 39, No. 2, pp. 117–120, March–April, 1998.
Rights and permissions
About this article
Cite this article
Berezin, Y.A., Spodareva, L.A. Slow motion of a granular layer on an inclined plane. J Appl Mech Tech Phys 39, 261–264 (1998). https://doi.org/10.1007/BF02468092
Received:
Issue Date:
DOI: https://doi.org/10.1007/BF02468092