Abstract
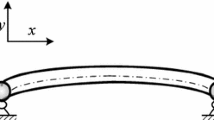
Based on the Hamilton's principle for elastic systems of changing mass, a differential equation of motion for viscoelastic curved pipes conveying fluid was derived using variational method, and the complex characteristic equation for the viscoelastic circular pipe conveying fluid was obtained by normalized power series method. The effects of dimensionless delay time on the variation relationship between dimensionless complex frequency of the clamped-clamped viscoelastic circular pipe conveying fluid with the Kelvin-Voigt model and dimensionless flow velocity were analyzed. For greater dimensionless delay time, the behavior of the viscoelastic pipe is that the first, second and third mode does not couple, while the pipe behaves divergent instability in the first and second order mode, then single-mode flutter takes place in the first order mode.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Chen S S. Flow induced in-plane instabilities of curved pipes[J].Nuclear Engineering and Design, 1972,23 (1): 29–38.
Chen S S. Out-of-plane vibration and stability of curved tubes conveying fluid[J].Journal of Applied Mechanics, ASME, 1973,40 (2): 362–368.
Misra A K, Paidoussis M P, Van K S. On the dynamics of curved pipes transporting fluid—Part I: Inextensible theory[J].Journal of Fluids and Structures, 1988,2 (3): 221–244.
Aithal R, Steven Gipson G. Instability of damped curved pipes[J].Journal of Applied Mechanics, ASME, 1993,116 (1): 77–90.
Wei Fayuan, Huang Yuying, Ren Zhiliang,et al. A new matrix method for solving problems of curved pipes conveying fluid[J].Acta Mechanica Solida Sinica, 2000,21 (1): 33–39 (in Chinese).
Ni Qiao, Zhang Huilan, Huang Yuying,et al. Differential quadrature method for the stability analysis of semi-circular pipe conveying fluid with spring support[J].Engineering Mechanics, 2000,17 (6): 59–64 (in Chinese).
Wang Zhongmin, Zhao Fengqun, Feng Zhenyu,et al. The dynamic behaviors of viscoelastic pipes conveying fluid with the Kelvin model[J].Acta Mechanica Solid Sinica, 2000,13 (3): 262–270.
Zhao Fengqun, Wang Zhongmin, Feng Zhenyu. Analysis of the dynamic behaviors of viscoelastic pipes conveying fluid with three-parameter solid model[J].Acta Mechanica Solida Sinica, 2002,23 (4): 483–489 (in Chinese).
Mclver D B. Hamilton's principle for systems of changing mass[J].Journal of Engineering Mathematics, 1973,7 (3): 249–261.
Yang Tingqing.Viscoelasticity[M]. Huazhong University of technology Press, Wuhan, 1990: 12–27 (in Chinese).
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by SHEN Hui-shen
Project supported by the Science Foundation of Shaanxi Provincial Commission of Education (No. 03JK069)
Rights and permissions
About this article
Cite this article
Zhong-min, W., Zhan-wu, Z. & Feng-qun, Z. Stability analysis of viscoelastic curved pipes conveying fluid. Appl Math Mech 26, 807–813 (2005). https://doi.org/10.1007/BF02465432
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF02465432