Skip to main content
SpringerLink
Log in

Description and weno numerical approximation to nonlinear waves of a multi-class traffic flow LWR model

  • Published:
Applied Mathematics and Mechanics Aims and scope Submit manuscript

Abstract

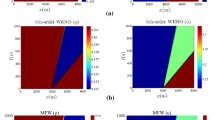
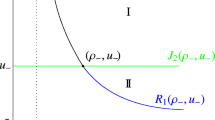
A strict proof of the hyperbolicity of the multi-class LWR (Lighthill-Whitham-Richards) traffic flow model, as well as the descriptions on those nonlinear waves characterized in the traffic flow problems were given. They were mainly about the monotonicity of densities across shocks and in rarefactions. As the system had no characteristic decomposition explicitly, a high resolution and higher order accuracy WENO (weighted essentially non-oscillatory) scheme was introduced to the numerical simulation, which coincides with the analytical description.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Dai Shiqiang, Feng Suwei, Gu Guoqing. Dynamics of traffic flow: its content, methodology and intent[J].J Nature, 1997,11(4):196–201 (in Chinese).

    Google Scholar 

  2. Helbing D. Traffic and related self-driven many-particle systems[J].Rev Mod Phys., 2001,73 (4):1067–1141.

    Article  Google Scholar 

  3. Lighthill M H, Whitham G B. On kinematics wave (II)—a theory of traffic flow on long crowded roads[J].Proc Roy Soc London, Ser A, 1955,22:317–345.

    MathSciNet  Google Scholar 

  4. Richards P I. Shock waves on the highway[J].Operations Research, 1956,4(2):42–51.

    Article  MathSciNet  Google Scholar 

  5. Wong G C K, Wong S C. A multi-class traffic flow model—an extension of LWR model with heterogeneous drivers[J].Transpn Res A, 2002,36(9):827–841.

    Google Scholar 

  6. Harten A, Engquish B, Osher S,et al Uninrmly high order essentially non-oscillatory schemes III[J].J Comput Phys, 1987,71(2):231–303.

    Article  MathSciNet  MATH  Google Scholar 

  7. Jiang G, Shu C W. Efficient implementation of weighted ENO schemes[J].J Comput Phys, 1996,126(1):202–228.

    Article  MathSciNet  MATH  Google Scholar 

  8. Liu X D, Osher S, Chan T. Weighted essentially nonoscillatory schemes[J].J Comput Phys, 1994,115(1):200–212.

    Article  MathSciNet  MATH  Google Scholar 

  9. Shu C W. Lecture Notes in Mathematics-Essentially Non-oscillatory and Weighted Essentially Non-oscillatory Schemes for Hyperbolic Conservation Laws[R]. 1697, Springer, Cetraro, Italy, 1997,329–432.

    Google Scholar 

  10. Whitham G B.Linear and Nonlinear Waves[M]. John Wiley and Sons, NY, 1974.

    MATH  Google Scholar 

  11. Lax P D. Shock Waves and Entropy[A]. In: Zarantonello E A (ed).Nonlinear Functional Analysis[C]. Academic Press, New York, 1971.

    Google Scholar 

  12. Lax P D.Hyperbolic Systems of Conservation Laws and the Mathematical Theory of Shock Waves[M]. SIAM, Philadelphia, 1973.

    MATH  Google Scholar 

  13. Toro E F.Riemann Solvers and Numerical Methods for Fluid Dynamics[M]. Springer-Verlay, Berlin, 1999.

    MATH  Google Scholar 

  14. Shu C W. TVB uniformly high order scheme for conservation laws[J].Mathematics of Computation, 1987,49(179):105–121.

    Article  MathSciNet  MATH  Google Scholar 

  15. Shu C W. Total-variation-diminishing time discretizations[J].SIAM Journal on Scientific and Statistical Computation, 1988,9(4):1073–1084.

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Shanghai Institute of Applied Mathematics and Mechanics, Shanghai University, 200072, Shanghai, P. R. China

    Zhang Peng (Associate Professor, Doctor) & Dai Shi-qiang

  2. Department of Mathematics, University of Science & Technology of China, 230026, Hefei, P. R. China

    Zhang Peng (Associate Professor, Doctor) & Liu Ru-xun

Authors
  1. Zhang Peng
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Dai Shi-qiang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Liu Ru-xun
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Zhang Peng.

Additional information

Contributed by DAI Shi-qiang

Project supported by the National Natural Science Foundation of China (Nos. 10472064, 10371118); the Post-Doctoral Science Foundation of China (No. 2003034254) and the Special Fund for PhD Program of Education Ministry of China (No. 20040280014)

Rights and permissions

Reprints and permissions

About this article

Cite this article

Peng, Z., Shi-qiang, D. & Ru-xun, L. Description and weno numerical approximation to nonlinear waves of a multi-class traffic flow LWR model. Appl Math Mech 26, 691–699 (2005). https://doi.org/10.1007/BF02465418

Download citation

  • Received:

  • Revised:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF02465418

Key words

Chinese Library Classification

2000 Mathematics Subject Classification

Search

Navigation