Skip to main content
SpringerLink
Log in

Stability and convergence of Dufort-Frankel-type difference schemes for a nonlinear Schrödinger-type equation

  • Published:
Lithuanian Mathematical Journal Aims and scope Submit manuscript

Abstract

We consider a first boundary problem for the nonlinear Schrödinger equation

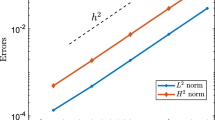
$$\frac{{\partial u}}{{\partial t}} = ia\frac{{\partial ^2 u}}{{\partial x^2 }} + f(u,u*)u.$$

The convergence of a three-layer explicit difference scheme in theC andW 21 norms is proved. The stability of the scheme with respect to the initial data in the same norms is proved. To justify the convergence and stability we use grid analogues of the energy-preservation laws and grid multiplicative inequalities. The relation 2|a|τ/h 2≤ν<1 is assumed for the grid stepsizes.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. A. P. Sukhorukov,Nonlinear Interactions of Waves in Optics and Radiophysics [in Russian], Nauka, Moscow (1988).

    Google Scholar 

  2. Yu. N. Karamzin, A. P. Sukhorukov, and V. A. TrofimovMathematical Modeling in Nonlinear Optics [in Russian], Moscow Univ. Press, Moscow (1989).

    Google Scholar 

  3. Yu. B. Gaididei, K. Ø. Rasmussen, and P. L. Christiansen, Nonlinear excitations in two-dimensional molecular structures with impurities,Phys. Rev. E,52 (1995).

  4. O. Bang, P. L. Christiansen, K. Ø. Rasmussen, and Yu. B. Gaididei, The role of nonlinearity in modelling energy transfer in Scheibe aggregates, in:Nonlinear Excitations in Biomolecules, M. Peyard (Ed.), Springer and Les Editions de Physique Les Ulis (1995), pp. 317–336.

  5. Lixin Wu, DuFort-Frankel-type methods for linear and nonlinear Schrödinger equations,SIAM J. Numer. Anal.,33, 1526–1533 (August 1996).

    Article  MATH  MathSciNet  Google Scholar 

  6. W. Dai, Absolute stable explicit and semi-explicit schemes for Schrödinger equations,Math. Numer. Sinica,11, 128–131 (1989).

    MATH  MathSciNet  Google Scholar 

  7. W. Dai, An unconditionally stable three-level explicit difference scheme for the Schrödinger equation with a variable coefficient,SIAM J. Numer. Anal.,29, 174–181 (1992).

    Article  MATH  MathSciNet  Google Scholar 

  8. F. Ivanauskas, Multiplicative estimate of the norm of a function inC in terms of norms inL 2,W n2 , and the convergence of difference methods for nonlinear evolution equations.Liet. Mat. Rinkinys,31, 311–322 (1991).

    MATH  MathSciNet  Google Scholar 

  9. F. Ivanauskas, Difference schemes for nonlinear equations of Schrödinger and parabolic types.Liet. Mat. Rinkinys,30, 247–260 (1990).

    MATH  MathSciNet  Google Scholar 

  10. M. Radžiūnas, On convergence and stability of difference schemes for nonlinear Schrödinger-type equations,Lith. Math. J.,36, 224–244 (1996).

    Article  Google Scholar 

  11. R. Čiegis, On the convergence inC norm of symmetric difference schemes for nonlinear evolution problems,Lith. Math. J.,32, 187–205 (1992).

    Google Scholar 

  12. V. V. Drits, Conservative difference schemes in nonlinear optics problems. I,Differents. Uravn.,27, 1153–1161 (1991).

    MATH  MathSciNet  Google Scholar 

  13. T. R. Taha, A numerical scheme for the nonlinear Schrödinger equation,Comput. Math. Appl.,22, 77–84 (1991).

    Article  MATH  Google Scholar 

  14. Y. Tourigny, Some pointwise estimates for the finite element solution of a radial nonlinear Schrödinger equation on a class of nonuniform grids,Numer. Methods Partial Differential Equations,10, 757–769 (1994).

    Article  MATH  MathSciNet  Google Scholar 

  15. Y. Tourigny, OptimalH 1 estimates for two time-discrete Galerkin approximations of a nonlinear Schrödinger equation,IMA J. Numer. Anal.,11, 509–523 (1991).

    MATH  MathSciNet  Google Scholar 

  16. G. D. Akrivis and V. A. Dougalis, On a class of conservative, highly accurate Galerkin methods for the Schrödinger equation,Math. Model. Numer. Anal.,25, 643–670 (1991).

    MATH  MathSciNet  Google Scholar 

  17. O. Karakashian, G. D. Akviris, and V. A. Dougalis, On optimal order error estimates for the nonlinear Schrödinger equation,SIAM J. Numer. Anal.,30, 377–400 (April 1993).

    Article  MATH  MathSciNet  Google Scholar 

  18. M. V. Vladimirov, On solvability of a mixed problem for a nonlinear Schrödinger type equation,Dokl. Akad. Nauk SSSR,275, 780–783 (1984).

    MATH  MathSciNet  Google Scholar 

  19. J.-L. Lions,Quelques Méthodes de Résolution des Problèmes aux Limites Non Linéaires, Paris (1969).

  20. A. A. Amosov and A. A. Zlotnik, A difference scheme for equations of motion of one-dimensional viscous barotropic gas, in:Computing Processes and Systems, Nauka, Moscow (1986), pp. 192–219.

    Google Scholar 

  21. A. A. Samarskii and V. B. Andreev,Difference Methods for Elliptic Equations [in Russian], Nauka, Moscow (1976).

    Google Scholar 

Download references

Authors
  1. F. Ivanauskas
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. M. Radžiūnas
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Vilnius University, Naugarduko 24, 2600 Vilnius, Lithuania. Translated from Lietuvos Matematikos Rinkinys, Vol. 37, No. 3, pp. 334–352, July–September, 1997.

Translated by V. Mackevičius

Rights and permissions

Reprints and permissions

About this article

Cite this article

Ivanauskas, F., Radžiūnas, M. Stability and convergence of Dufort-Frankel-type difference schemes for a nonlinear Schrödinger-type equation. Lith Math J 37, 249–263 (1997). https://doi.org/10.1007/BF02465356

Download citation

  • Received:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF02465356

Keywords

Search

Navigation