Abstract
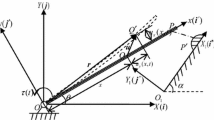
The dynamic behavior of a two-degree-of-freedom oblique impact system consisted of two pendulums with non-fixed impact positions is investigated. The relations between the restitution coefficient, the friction coefficient, as well as other parameters of the system and the states before or after impact, are clarified in this oblique impact process. The existence criterion of single impact periodic-n subharmonic motions is deduced based on the Poincaré map method and the oblique impact relations with non-fixed impact positions. The stability of these subharmonic periodic motions is analyzed by the Floquet theory, and the formulas to calculate the Floquet multipliers are given. The validity of this method is shown through numerical simulation. At the same time, the probability distribution of impact positions in this oblique system with non-fixed impact positions is analyzed.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Shaw S W, Homes P J. A periodically forced piecewise linear oscillator[J].Journal of Sound and Vibration, 1983,90 (1): 129–155.
Shaw S W The dynamics of harmonically excited system having rigid amplitude constraints, part I—subharmonic motions and local bifurcations[J].Transactions of ASME, Journal of Applied Mechanics, 1985,52 (2): 453–458.
Whiston G S. The vibro-impact response of a harmonically excited and preloaded one-dimensional linear oscillator[J].Journal of Sound and Vibration, 1987,115 (2): 303–319.
Whiston G S. Global dynamics of a vibro-impacting linear oscillator[J].Journal of Sound and Vibration, 1987,118 (3): 395–424.
Li Qunhong, Lu Qishao. Analysis to motions of a two-degree-of-freedom vibro-impact system [J].Acta Mechanics Sinica, 2001,33 (6): 776–786.
Jin, D P, Hu H Y. Periodic impacting motions and their stability of a dual component system [J].Acta Mechanics Sinica, 1997,13 (4): 427–447.
Strong W J.Impact Mechanics [M]. Cambridge University Press, Cambridge, 2000, 1–280.
Stronge W J. Friction in collisions: resolution of a paradox[J].Journal of Applied Physics, 1991,69 (2): 610–612.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by CHEN Yu-shu
Project supported by the National Natural Science Foundation of China (Nos. 19990510 and 10432010)
Rights and permissions
About this article
Cite this article
Li, J., Qi-shao, L. & Qi, W. Dynamic analysis of two-degree-of-freedom oblique impact system with non-fixed impact positions. Appl Math Mech 26, 882–892 (2005). https://doi.org/10.1007/BF02464237
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF02464237
Key words
- impact with non-fixed position
- oblique impact
- subharmonic motion
- existence
- stability
- probability distribution