Abstract
A biological system consisting of a population of cells suspended in a liquid substrate is considered. The general problem addressed in the paper is the derivation of the kinetic pattern of population growth as a statistical effect of a very large number of elementary interactions between a single cell and the molecules of nutrient in substrate. Solution of the problem is obtained in the form of equation expressing the population growth ratec as a function of substrate concentration,C s. The analytical expression derived is applied to a real bacterial population (Escherichi coli) and kinetic patterns are theoretically computed. The major findings, expressed roughly, without nuances, are: (i) the concentration of nutrient at the cell membrane,C c, can only be equal to either 0 (for theC s below some threshold valueC *) orC s (forC s>C *); (ii) the Michaelis-Menten-Monod kinetics observed in experiments is an artifact: the pure (not contaminated by foreign factors) dependence ofc onC s is actually such that the functionc=c(C s) has practically linear increase whenC s<C *, and is constant,c=c(C *)=const, whenC s>C *; (iii) the Liebig principle is strictly fulfilled: up to a feasible accuracy of observation, under no circumstances can population growth be limited (controlled) by more than one substrate component—replacement of a limiting component for another one is an instant event rather than a gradual process.
Similar content being viewed by others
Abbreviations
- c :
-
(1)
- a, b :
-
(3)–(4)
- μ,C s, λ,u :
-
Section 1
- ρ, ρs :
-
Point 2.1
- λ1, λ2 :
-
(5) (6), (9)–(10)
- λ0 :
-
Point 2.4
- σ, τ0 :
-
Point 2.1
- D, N, M,u ρ,u ∞ :
-
Point 2.2
- η,T, A, B :
-
(7)–(8)
- K, E, T o :
-
Section 3, (16)
- ω1, ω2, ω:
-
Section 3, (20)
- t min,t min,\(\bar \rho \),\(\bar x_0 \) :
-
(20), (21)
- β, α:
-
(29)
- C (0)s :
-
Point 4.2
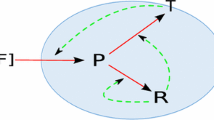
- C (m)s ,c max :
-
Fig. 2
References
Einstein, A. 1966.Collected Works (Russian edition), Vol. 3. Moscow: Nauka.
Frenkel, Y. I. 1948.Statistical Physics (in Russian). Moscow-Leningrad: U.S.S.R. Academy of Sciences.
Frobisher, M. 1965.Fundamentals of Microbiology (Russian edition). Moscow: Mir.
Fuxman, Y. L. 1981. On the law of reproduction of cell population.J. gen. Biol. XLII, (in Russian).
Fuxman, Y. L. 1992. Reproduction rate, feeding process, and Liebig limitations in cell populations—Part I.Bull. Math. Biol. 55, No. 1.
Gorlenko, V. M., S. I. Kuznetsov and G. L. Dubinina. 1977.Ecology of Aquatic Microorganisms (in Russian). Moscow: Nauka.
Handbook on Properties, Methods of Analysis, and Purification of Water (in Russian). 1980. Kiev: Naukova Dumka.
Korn, G. A. and T. M. Korn. 1968.Mathematical Handbook. New York: McGraw-Hill.
Konstantinov, A. S. 1972.General Hydrobiology (in Russian). Moscow:Vyschaya Shcola.
Kuznetsov, S. I. 1970.Microflora of Lakes (in Russian). Leningrad: Nauka.
Pechurkin, N. S., N. V. Nikiforova and A. G. Degemermengy. 1982.Biophysiak No. 2 (in Russian).
Pirt, S. J. 1978.Fundamentals of Culturing Microorganisms and Cells (Russian edition). Moscow: Mir.
Shlegel, H. 1972.General Microbiology (Russian edition). Moscow: Mir.
Winberg, G. G. 1946. Respiration rate of bacteria.Adv. Mod. Biol. 21, (in Russian).
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Fuxman, Y.L. Reproduction rate, feeding process, and liebig limitations in cell populations—II. Bltn Mathcal Biology 57, 749–782 (1995). https://doi.org/10.1007/BF02461850
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1007/BF02461850