Skip to main content
SpringerLink
Log in

Stochastic prey-predator relationships: A random evolution approach

  • Published:
Bulletin of Mathematical Biology Aims and scope Submit manuscript

Abstract

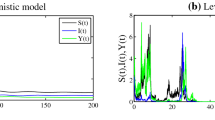
The formalism and results of the theory of random evolutions are used to establish and investigate a model for two randomly interacting populations. The asymptotic stability of the expected solution is studied and contrasted to that of the associated deterministic system.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Literature

  • Abramowitz, M. and I. A. Stegun. 1965. (Eds).Handbook of Mathematical Functions. New York: Dover.

    Google Scholar 

  • Bartlett, M. S. 1960.Stochastic Models in Ecology and Epidemiology. London: Methuen.

    Google Scholar 

  • Bécus, G. A. 1979. “Stochastic Prey-Predator Relationships: A Random Differential Equation Approach.”Bull. Math. Biol,41, 91–100.

    Article  MATH  MathSciNet  Google Scholar 

  • Bharucha-Reid, A. T. 1960.Elements of the Theory of Markov Processes and their Applications. New York: McGraw-Hill.

    Google Scholar 

  • Coppel, W. A. 1965.Stability and Asymptotic Behavior of Differential Equations. Boston: Heath.

    Google Scholar 

  • Gard, T. C. and D. Kannan. 1976. “On a Stochastic Differential Equation Modeling Prey-Predator Evolution.”J. Appl. Prob.,13, 429–443.

    Article  MATH  MathSciNet  Google Scholar 

  • Goel, N. S., S. C. Maitra and E. W. Montroll. 1971. “On the Volterra and Other Nonlinear Models of Interacting Populations.”Rev. Mod. Phys. 43, 321–376.

    Article  MathSciNet  Google Scholar 

  • —, and N. R. Dyn. 1974.Stochastic Models in Biology. New York: Academic Press.

    Google Scholar 

  • Gomatam, J. 1974. “A New Model of Interacting Populations—I: Two Species Systems.”Bull. Math. Biol.,36, 347–353.

    Article  MATH  Google Scholar 

  • Griego, R. and R. Hersh. 1971. “Theory of Random Evolutions with Applications to Partial Differential Equations.”TAMS,156, 405–418.

    Article  MATH  MathSciNet  Google Scholar 

  • Hersh, R. and M. Pinsky. 1972. “Random Evolutions are Asymptotically Gaussian.”Comm. Pure Appl. Math. 25, 33–44.

    MATH  MathSciNet  Google Scholar 

  • Kannan, D. 1976. “On Some Markov Models of Certain Interacting Populations.”Bull. Math. Biol.,38, 723–738.

    Article  MATH  MathSciNet  Google Scholar 

  • Kurtz, T. G. 1972. “A Random Trotter Product Formula.”Proc. AMS 35, 147–154.

    Article  MATH  MathSciNet  Google Scholar 

  • — 1973. “A Limit Theorem for Perturbed Operator Semigroups with Applications to Random Evolutions.”J. Funct. Anal. 12, 55–67.

    Article  MATH  MathSciNet  Google Scholar 

  • Lions, J. L. 1976.Sur Quelques Questions d'Analyse, de Mécanique, et de Contrôle Optimal. Montréal, Canada: Presses de l'U. de Montréal.

    Google Scholar 

  • Prajneshu, 1976a. “A Stochastic Model for Two Interacting Species.”Stoch. Proc. Appl. 4, 271–282.

    Article  MathSciNet  Google Scholar 

  • Prajneshu, 1976b. “Two-Species Systems in Random Environment.” To appear.

  • Soong, T. T. 1973.Random Differential Equations in Science and Engineering. New York: Academic Press.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Engineering Science, University of Cincinnati, 45221, Cincinnati, Ohio, USA

    Georges A. Bécus

Authors
  1. Georges A. Bécus
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Bécus, G.A. Stochastic prey-predator relationships: A random evolution approach. Bltn Mathcal Biology 41, 543–554 (1979). https://doi.org/10.1007/BF02458329

Download citation

  • Received:

  • Revised:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF02458329

Keywords

Search

Navigation