Skip to main content
SpringerLink
Log in

Asymptotic analysis of a class of nonlinear oscillation equation in electrical engineering

  • Published:
Applied Mathematics and Mechanics Aims and scope Submit manuscript

Abstract

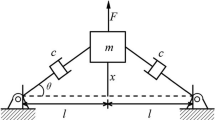
In the present paper, we investigate a class of nonlinear oscillation equations in electrical engineering by using the modified Krylov-Bogolyubov method presented in[1]. We obtain quantitatively the parameter range for the existence of a limit cycle and the amplitude of the limit cycle, and find that the limit cycle is unstable. All the results agree entirely with the known results given by qualitative analysis, and hence confirm the effectiveness of the above-mentioned asymptotic method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Dai Shi-qiang, Asymptotic analysis of strongly nonlinear oscillators,Appl. Math. and Mech. (English ed.),6, 5 (1985), 409–415.

    Article  MATH  MathSciNet  Google Scholar 

  2. Shen Jia-qi and Yu Buo-hua, Chaotic Behavior of a nonlinear perturbation equation,Acta Methematica Sinica,31, 2 (1988), 215–220. (in Chinese).

    MATH  MathSciNet  Google Scholar 

  3. Dai Shi-qiang and Zhuang Feng-qiang, Asymptotic solutions to nonlinear oscillation systems,Scientia Sinica (Ser. A)29, 7 (1986), 737-744.

    MATH  Google Scholar 

  4. Byrd, P. F. and M. D., Friedman,Handbook of Elliptic Integrals for Engineers and Scientists, 2nd ed., Springer, New York (1971).

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Fundamental Courses, North China Institute of Electric Power, Baoding

    Chen You-liang

  2. Shanghai Institute of Applied Mathematics and Mechanics, Shanghai University of Technology, Shanghai

    Dai Shi-qiang

Authors
  1. Chen You-liang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Dai Shi-qiang
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Projects Supported by Shanghai Natural Science Foundation

Rights and permissions

Reprints and permissions

About this article

Cite this article

You-liang, C., Shi-qiang, D. Asymptotic analysis of a class of nonlinear oscillation equation in electrical engineering. Appl Math Mech 15, 7–12 (1994). https://doi.org/10.1007/BF02451022

Download citation

  • Received:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF02451022

Key words

Search

Navigation