Abstract
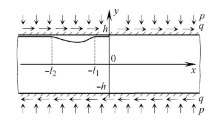
Stress analysis for an infinite strip weakened by periodic cracks is studied. The cracks were assumed in a horizontal position, and the strip was applied by tension “p” iny-direction. The boundary value problem can be reduced into a complex mixed one. It is found that the EEVM (eigenfunction expansion variational method) is efficient to solve the problem. The stress intensity factor at the crack tip and theT-stress were evaluated. From the deformation response under tension the cracked strip can be equivalent to an orthotropic strip without cracks. The elastic properties in the equivalent orthotropic strip were also investigated. Finally, numerical examples and results were given.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Savruk M P.Two-dimensional Problems of Elasticity for Body with Cracks[M]. Kiev: Nauka Dumka, 1981.
CHEN Yi-zhou. A survey of new integral equations in plane elasticity crack problem [J].Engng Fract Mech, 1995,51(5):387–394.
CHEN Yi-zhou, Lee K Y. An infinite plate weakened by periodic cracks[J].J Appl Mech, 2002,69(3):552–555.
Isida M, Usijima N, Kishine N. Rectangular plate, strips and wide plates containing internal cracks under various boundary conditions[J].Trans Japan Soc Mech Engrs, 1981,47:27–35.
Delameter W R, Herrmann G, Barnett D M. Weakening of elastic solid by a rectangular array of cracks[J].J Appl Mech, 1975,42(1):74–80.
Parton V Z, Perlin P I.Integral Equations in Elasticity [M]. Moscow: Mir, 1982.
Benthem J P, Koiter W T. Asymptotic approximations to crack problems[A]. In: G C Sih Ed.Mechanics of Fracture[C]. 1973,1:131–178.
Huang Y, Hu K X, Chandra A. Stiffness evaluation for solids containing dilute distributions of inclusions and microcracks[J].J Appl Mech, 1995,62(1):71–77.
Kachanov M. Elastic solids with many cracks and related problems[A]. In: J W Hutchinson, T Wu Eds.Advances in Applied Mechanics[C]. 1993,30:259–445.
CHEN Yi-zhou. An investigation of the stress intensity factor for a finite internally cracked plate by using variational method[J].Engng Fract Mech, 1983,17(5):387–394.
Wang W C, Chen J T. Stress analysis of finite interfacially cracked bimaterial plates by using variational method[J].Comput Methods Appl Mech Engrg, 1989,73:153–171.
Muskhelishvili N I.Some Basic Problems in the Theory of Elasticity [M]. Gronigen: Noordhoff, 1953.
CHEN Yi-zhou. Closed form solution of T-stress in plane elasticity crack problems[J].Internat J Solids and Structures, 2000,37(11):1629–1637.
Lekhnitsky S G.Theory of Elasticity of Anisotropic Elastic Body[M]. San Francisco: Holden-Day, 1963.
Author information
Authors and Affiliations
Additional information
Communicated by Wang Yin-bang
Foundation item: the National Natural Science Foundation of China (10272053)
Biography: Chen Yi-zhou (1935})
Rights and permissions
About this article
Cite this article
Yi-zhou, C. Stress analysis for an infinite strip weakned by periodic cracks. Appl Math Mech 25, 1298–1303 (2004). https://doi.org/10.1007/BF02438286
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF02438286