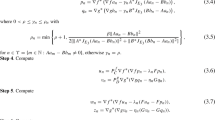Abstract
Kantorovich theorem was extended to variational inequalities by which the convergence of Newton iteration, the existence and uniqueness of the solution of the problem can be tested via computational conditions at the initial point.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Éaves B C. A locally quadratically convergent algorithm for computing stationary point[R]. Department of Operations Research, Stanford University, 1978.
Josephy N H. Newton's method for generalized equations[R]. Mathematics Research Center, University of Wisconsin, 1979.
Harker P T, Pang J S. Finite-dimensional variational inequalities and nonlinear complementarity problems: a survey of theory, algorithms and applications[J].Mathematical Programming, 1990,48 (2):161–220.
Robinson S M. Generalized equations and their solutions[J].Mathematical Programming Study, 1979,10(1):128–141.
Robinson S M. Strongly regular generalized equations[J].Mathematics of Operations Research, 1980,5(1):43–62.
Kantorovich L V. Functional analysis and applied mathematics[J].Uspehi Mat Nauk, 1948,3(6): 89–185.
Ortega J M, Rheinboldt W C.Iterative Solutions of Nonlinear Equations in Several Variables[M]. New York: Academic Press, 1970.
Stampacchia G. Variational inequalities[A]. In: Stampacchia G Ed.Theory and Applications of Monotone Operators, Proceedings of the NATO Advanced Study Institute[C]. Venice: Edizioni Oderisi, Gubbio, 1968, 102–192.
Rall L BComputational Solution of Nonlinear Operator Equations[M]. New York: Wiely, 1969.
Alefeld G E, Herzberger J.Introduction to Interval Computations[M]. New York and London: Academic Press, 1983.
Author information
Authors and Affiliations
Additional information
Communicated by Wu Qi-guang, Original Member of Editorial Committee, AMM
Biography: Wang Zheng-yu (1971})
Rights and permissions
About this article
Cite this article
Zheng-yu, W., Zu-he, S. Kantorovich theorem for variational inequalities. Appl Math Mech 25, 1291–1297 (2004). https://doi.org/10.1007/BF02438285
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF02438285