Abstract
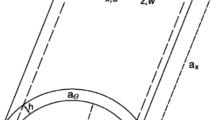
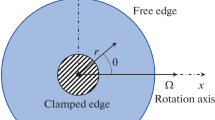
The three-dimensional frame is simplified into flat plate by the method of quasiplate. The nonlinear relationships between the surface strain and the midst plane displacement are established. According to the thin plate nonlinear dynamical theory, the nonlinear dynamical equations of three-dimensional frame in the orthogonal coordinates system are obtained. Then the equations are translated into the axial symmetry nonlinear dynamical equations in the polar coordinates system. Some dimensionless quantities different from the plate of uniform thickness are introduced under the boundary conditions of fixed edges, then these fundamental equations are simplified with these dimensionless quantities. A cubic nonlinear vibration equation is obtained with the method of Galerkin. The stability and bifurcation of the circular three-dimensional frame are studied under the condition of without outer motivation. The contingent chaotic vibration of the three-dimensional frame is studied with the method of Melnikov. Some phase figures of contingent chaotic vibration are plotted with digital artificial method.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
NIE Guo-hua, LIU Ren-huai. Nonlinear characteristic relationships of rectangular reticulated shallow shells[J].Civil Engineering Transaction, 1995,28,(1):12–21. (in Chinese)
XIAO Tan, LIU Ren-huai. Nonlinear bending theory of diagonal square pyramid reticulated shallow shells[J].Applied Mathematics and Mechaincs (English Edition), 2001,22(7):747–755.
ZHU Zhong-yi, DONG Shi-lin, GAO Bo-qing. The geometrically nonlinear analysis of folded plate latticed vault[J].Industry Architecture, 2001,31(2):51–59. (in Chinese)
DONG, Shi-lin, ZHANG Zhi-hong, LI Yuan-qi. Research on geometrical nonlinear finite element method of spatial reticulated structures[J].Calculate Mechanics Transaction, 2002,19(3):365–368. (in Chinese)
NIE Guo-hua. Non-linear vibration of rectangular reticulated shallow shell structures[J].Applied Mathematics and Mechanics (English Edition), 1994,15(6):525–535.
GAO Bo-qing, DONG Shi-lin. Dynamic property analysis of folded plate type latticed shell[J].Architecture Structure Transaction, 2002,23(1):53–57. (in Chinese)
HAN Qiang, ZHANG Shan-yuan, YANG Gui-tong. The study on the chaotic motion of a nonlinear dynamic system[J].Applied Mathematics and Mechaincs (English Edition), 1999,20(8):830–836.
Moon F C, Shaw S W. Chsotic vibration of a beam with nonlinear boundary conditions[J].Nonlinear Mechanics, 1983,18(6):465–477.
ZHAO Yan-ying, WANG Xin-zhi, ZHAO Yong-gang,et al. The nonlinear bending analysis of the circular three-dimensional frame[J].Journal of Lanzhou University of Technology, 2003,29(3): 143–145. (in Chinese)
Author information
Authors and Affiliations
Additional information
Contributed by Yeh Kai-yuan
Foundation item: the National Natural Science Foundation of Gansu Province (ZS021-A25-007-Z)
Biography: Wang Xin-zhi (1940∼), Professor
Rights and permissions
About this article
Cite this article
Xin-zhi, W., Gang, W., Yan-ying, Z. et al. Nonlinear dynamical stability analysis of the circular three-dimensional frame. Appl Math Mech 25, 367–372 (2004). https://doi.org/10.1007/BF02437519
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF02437519