Abstract
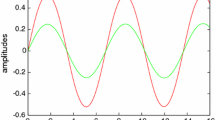
Nonlinear normal modes in a two degrees of freedom asymmetric system with cubic nonlinearities as singularity occurs in the system are studied, based on the invariant space in nonlinear normal modes and perturbation technique. Emphasis is placed on singular characteristics as the linear coupling between subsystems degenerated. For nonresonances, it is analytically presented that a single-mode motion and localization of vibrations occur in the system, and the degree of localization relates not only to the coupling stiffness between oscillators, but also to the asymmetric parameter. The parametric threshold value of localization is analytically given. For 1:1 resonance, there exist bifurcations of normal modes with nonlinearly coupling stiffness and asymmetric parameter varying. The bifurcating set on the parameter and bifurcating curves of normal modes are obtained.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Guchenheimer J, Holmes P.Nonlinear Oscillation, Dynamical System and Bifurcation of Vector Fields[M]. New York: Springer-Verlag, 1983.
LU Qi-shao.Bifurcations and Singularity[M]. Shanghai: Shanghai Press of Science and Technology, 1995. (in Chinese)
Nayfeh A H, Mook D T.Nonlinear Oscillations[M]. New York: John Wiley & Sons Inc, 1979.
Winggins S.Introduction to Applied Nonlinear Dynamical Systems and Chaos[M]. New York: Springer-Verlag, 1990.
Chen Y S, Langford W F. The subharmonic bifurcation solution of nonlinear Mathieu's equation and Euler dynamically buckling problem[J].Acta Mech Sinica, 1998,19(3):522–532.
Iooss G, Joseph D D.Elementary Stability and Bifurcation Theory[M]. New York: Springer-Verlag, 1980.
Shaw S W, Pierre C. Normal modes for nonlinear vibration systems[J].Journal of Sound and Vibration, 1993,164(1):85–124.
XU Jian, LU Qi-shao, HUANG Ke-lei. Nonlinear normal modes and their superposition in a two degrees of freedom asymmetric system with cubic nonlinearities[J].Applied Mathematics and Mechanics (English Ed.), 1998,19(12):1167–1177.
Anderson P W. Absence of diffusion in certain random lattices[J].Physical Review, 1958,109 (12):1492–1505.
Hodges C H. Confinement of vibration by structural chains[J].Journal of Sound and Vibration, 1982,82(2):411–424.
Pierre C, Dowell E H. Localization of vibration by structural irregularity[J].Journal of Sound and Vibration, 1987,114(3):549–564.
Pierre C. Model localization and eigenvalue loci veering phenomena in disordered structures[J].Journal of Sound and Vibration, 1988,126(3):485–502.
Pierre C. Weak and strong vibration localization in disordered structures: a statistical investigation [J].Journal of Sound and Vibration, 1990,139(1):111–132.
CHEN Yu-shu.Nonlinear Vibrations[M]. Tianjin: Tianjin Press of Science and Technology, 1983. (in Chinese)
Golubisky M, Stewart I, Schaeffer D G.Singularities and Groups in Bifurcation Theory[M]. Vol I and Vol II. New York: Springer-Verlag, 1988.
Caughey T K, Vakakis A, Sivo J M. Analytical study of similar normal modes and their bifurcations in class of strongly non-linear systems[J].Int J Non-Linear Mechanics 1990,25(5):521–533.
Author information
Authors and Affiliations
Additional information
Communicated by Chen Yu-shu
Foundation item: the National Natural Science Foundation of China (10072039, 19990510)
Biography: Xu Jian (1961-)
Rights and permissions
About this article
Cite this article
Jian, X., Qi-shao, L. & Ke-lei, H. Singular characteristics of nonlinear normal modes in a two degrees of freedom asymmetric systems with cubic nonlinearities. Appl Math Mech 22, 972–982 (2001). https://doi.org/10.1007/BF02436397
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF02436397
Key words
- asymmetric system
- nonlinear normal mode
- localization of vibration
- bifurcation of normal mode
- nonlinear dynamics