Abstract
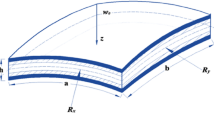
Based on the variation and harmonic equations and by taking the maximum amplitude of the shell center as the perturbation parameter, nonlinear vibration of thin shallow conic shells under combined action of peripheral moment and transverse loads was solved. The linear natural frequency can be got by the first-order approximation and the more accurate nonlinear frequency is got by the second-order approximation under the action of static loads. Meanwhile the third-order approximate analytic expression is given for describing the nonlinear relation between nature frequency and peripheral moment, transverse loads, amplitude, base angle under the small deformation. Within some range, the complex and regularity of the nonlinear relation can be directly observed from the numeric results.
Similar content being viewed by others
References
LI Shi-rong, SONG Xi, ZHAO Yong-gang. The nature frequency of annular plate with variable thickness under the temperature loads[J].Engineering Mechanics, 1995,12(1):58–65. (in Chinese)
WANG Xin-zhi, ZHAO Yong-gang, YEH Kai-yuan. Non-symmetrical large deformation of a shallow thin conical shell[J].Applied Mathematics and Mechanics (English Edition), 1998,19 (10):917–928.
WANG Yong-gang, LÜ Ying-min. Nonlinear vibration of flexible shallow spherical shells under the static loads[J].Journal of Nonlinear Dynamics in Science and Technoology, 1999,6(2):95–101. (in Chinese)
ZHOU You-he, ZHENG Xiao-jing. Large amplitude vibration in the vicinity of the nonlinear equilibrium configuration of the circular plate subjected static load[J].Journal of Nonlinear Dynamics in Science and Technology, 1994,1(4):185–194. (in Chinese)
ZHAO Yong-gang. Nonlinear vibration problem of circular plate under multiple loads[J]Journal of Gansu University of Technology, 1997,23(4):92–94 (in Chinese)
ZHAO Yong-gang, MA Lian-sheng, WANG Xin-zhi. Large amplitude vibration of a shallow thin conic shell subjected to temperature load[J].Journal of Lanzhou Railway University, 2001,20(4): 21–26 (in Chinese)
HU Yu-da. The general solution of the nonlinear vibration of the ideal conductive thin-plate in a magnetic field[J].Journal of Nonlinear Dynamics in Science and Technology, 1999,6(4):338–342. (in Chinese)
DU Guo-jun. Large amplitude vibration of flexible circular plates under static loads[J].Journal of Applied Mechanics, 1994,11(4):43–50 (in Chinese)
WANG Xin-zhi, WANG Lin-xiang, HU Xiao-fang. Nonlinear vibration of circular corrugated plates [J].Applied Mathematics and Mechanics (English Edition), 1987,8(3):241–250.
WANG Xin-zhi, MA Lian-sheng, ZHAO Yong-gang,et al.. Nonlinear vibration of shallow conic shells subjected to static load[A]. In: CHIEN Wei-zang Ed.Proceedings of the 3rd International Conference on Nonlinear Mechanics[C]. Shanghai: Shanghai University Press, 1998,377–380.
Author information
Authors and Affiliations
Additional information
Contributed by Yeh Kai-yuan
Foundation item: the Natural Science Foundation of Gansu Province of China (ZS022-A25-O22)
Biography: Zhao Yong-gang (1967≈)
Rights and permissions
About this article
Cite this article
Yong-gang, Z., Xin-zhi, W. & Kai-yuan, Y. Nonlinear vibration of thin shallow conic shells under combined action of peripheral moment and transverse loads. Appl Math Mech 24, 1381–1389 (2003). https://doi.org/10.1007/BF02435578
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF02435578