An evaluation of two classes of shock hydrodynamic codes

Abstract

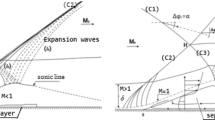
The accuracy of four industrial shock hydrodynamics codes for blast environments in baffled systems is evaluated based on the shadowgraph data of Reichenbach and Kuhl (1992,3). Both problems involve a planar shock passing through a baffled channel. The numerical methods employed in these codes are representative of two classes, namely, the set of high-resolution schemes advanced in the 1980's, and the classical finite-difference schemes from the late 1960's. The four codes are: (1) the AMR code based on the higher-order Godunov scheme with adaptive grids, (2) the FEM-FCT code based on the flux-corrected transport scheme with unstructured grids, (3) and (4) the finite-difference based HULL and SHARC codes with fixed grids. From the comparisons of these calculations it is concluded that the high-resolution schemes: (1) calculate sharper shocks and sharper density profiles across vortices, (2) predict shear layer rollup forming coherent structures in the spiral vortices immediately down-stream of every baffle, and (3) predict development of inviscid instabilities from these shear layers that, upon interaction with the reverberating shocks in the system, quickly become ‘turbulent’. The finite-difference codes predict essentially laminar behavior for the shear layers. Comparisons with shadowgraph data suggest that both classes of codes are able to predict shock reflections and diffractions in the baffled systems. The high-resolution codes give better agreement in the spiral vortices and the shear layers. As expected, turbulent flow features involving highly dissipative flow fields are not predicted by the high-resolution codes.