References
Diese Benennung ist von HerrnWeingarten eingeführt worden (Journal f. r. u. ang. Math., Bd. 94, S. 182). HerrWeingarten nennt aber Biegungsinvarianten nur diejenigen Functionen, welche wir später (No 13) als Gaussische Biegungsinvarianten bezeichnen. Es scheint nämlich zweckmässig, für alle Differentialinvarianten einer unendlichen Gruppe, die wir im Folgenden (No 4) definieren werden, den gemeinsamen Namen «Biegungsinvarianten» einzuführen.
Mathem. Annal., Bd. 24, S. 574–575.
Es handelt sich natürlich um die Anzahl derunabhängigen Biegungsinvarianten, wobei zu bemerken ist, dass jeN Biegungsinvarianten, etaI 1, I2, … IN, dann und nur dann von einander unabhängig sind, wenn keine Identität von der FormF(I 1, I2, … IN)=0 besteht.
Dieser Satz ist analog dem entsprechenden Satze aus der Theorie der endlichen continuierlichen Transformationsgruppen. Siehe:Sophus Lie,Theorie der Transformationsgruppen. Erster Abschnitt. Unter Mitwirkung von Dr.F. Engel bearbeitet. Leipzig, Teubner. 1888. S. 547, Theorem 94. Die Formulierung des Theorems I ist eine etwas abweichende von der des Theorems 94.
Sophus Lie, Mathem. Ann., Bd. 24:Über Differentialinvarianten. S. 564 ff.
Sophus Lie,Über Differentialinvarianten, S. 553 und Christiania Videnskabsselskabs Forhaudlinger 1883,Über unendliche continuierliche Gruppen, S. 4.
Sophus Lie.Über Differentialinvarianten, S. 574.
Gauss.Disquisitiones generales circa superficies curvas.
F. Bessel:Über die Entwickelung der höheren Differentiale zusammengesetzter und implicieter Functionen. Diss. Jena 1872.
Man bemerke, dass erstens jedes Glied der Summe, für welchesi oderk negativ ausfällt, gleich Null ist und zweitens die untere Grenze der Summation stets kleiner, als die obere ist. Bezeichnet man also mita ik alles, was unter dem Zeichen der Summe steht, so kann man schreiben:\(\begin{gathered} \mathop {\sum '_i }\limits_{\mu - 1}^{n + 1} \mathop {\sum '_k }\limits_{\nu - 1}^{n + 1 - i} a_{ik} = \mathop {\sum _i }\limits_{\nu - 1}^{n + 1 - i} \left( {a_{i,\nu - 1} + \ldots + a_{i,n - i} + a_{i,n + 1 - i} } \right) \hfill \\ = \mathop {\sum '_i }\limits_{\mu - 1}^n \mathop {\sum '_k }\limits_{\nu - 1}^{n - i} a_{ik} + \mathop {\sum _k }\limits_{\nu - 1}^{ - 1} a_{n + 1,k} + \mathop {\sum _i }\limits_{\mu - 1}^{n + i} a_{i,n + 1 - i,} \hfill \\ \end{gathered} \) woraus folgt:\(\mathop {\sum '_i }\limits_{\mu - 1}^{n + 1} \mathop {\sum '_k }\limits_{\nu - 1}^{n + 1 - i} a_{ik} = \mathop {\sum _i }\limits_{\mu - 1}^n \mathop {\sum _k }\limits_{\nu - 1}^{n - i} a_{ik} + \mathop {\sum _i }\limits_{\mu - 1}^{n + 1} a_{i,n + 1 - i,} \) was eben bewiesen werden sollte.
In ähnlicher Weise haben wir:\(\mathop {\sum '_i }\limits_{\mu - 1}^{n + 1} \mathop {\sum '_k }\limits_{n + 1 - \mu }^{n + 1 - i} a_{ik} = \mathop {\sum _k }\limits_{n + 1 - \mu }^{n + 2 - \mu } a_{\mu - 1,k} + \mathop {\sum _k }\limits_{n + 1 - \mu }^{n + 1 - \mu } a_{\mu k} + \mathop {\sum _k }\limits_{n + 1 - \mu }^{n - \mu } a_{\mu + 1,k} + \ldots + \mathop {\sum _k }\limits_{n + 1 - \mu }^0 a_{n + 1,k} ;\) weil aber nicht gleichzeitigi=μ−1, undk=n+1−μ sein können, so ergiebt sich:\(\mathop {\sum '_i }\limits_{\mu - 1}^{n + 1} \mathop {\sum '_k }\limits_{n + 1 - \mu }^{n + 1 - i} a_{ik} = a_{\mu - 1,n + 2 - \mu } + a\alpha _{\mu ,n + 1 - \mu } + a_{\mu + 1,n - \mu } + \ldots + a_{n + 1,0} = \mathop {\sum _i }\limits_{\mu - 1}^{n + 1} a_{i,n + 1 - i} ,\) was eben zu beweisen war.
Diese Gleichungen sind die etwas anders geschriebenen Gleichungen (16).
Sind hier die ωkls von denx 1, x2, …, xn unabhängig, so bilden die infinitesimalen TransformationenX kf eineq-gliedrige Gruppe, deren Betrachtung man imLie'schen Lehrbuche:Theorie der Transformationsgruppen. Erster Abschnitt. Kapitel 28. findet.
Es muss wenigstens eine solche Function ϕ geben. Angenommen, dass alle Lösungen der GleichungenX lf=0 (l=1, 2, …,q−1) auch die GleichungY qf=0 befriedigten, so kommen wir zum Schlusse, dass das System (a)n−q+1 unabhängige Lösungen besitzt, was unmöglich ist.
Doch scheint dieser Beweis nicht ganz streng zu sein; deshalb wollen wir einen anderen angeben. Soll unsere Identität (26) bestehen, so müssen die Coefficienten der Differentialquotienten vonf alle identisch Null werden. Insbesondere giebt der Coefficient von\(\frac{{\partial f}}{{\partial E_{i',n - i'} }}:\):\(\begin{gathered} \left( a \right)\mathop \sum \limits_0^{\lambda + 1} \left\{ {e_{\lambda \mu } \left( {2i'_{\mu - 1} + i'_\mu } \right)\left( {n - i'} \right)_{\lambda + 1 - \mu } E_{i' - \mu + 1,n - i' - \lambda - 1 + \mu } } \right. \hfill \\ \left. { + \bar e_{\lambda \mu } \left( {n - i'} \right)_{\lambda + 1 - \mu } \left( {2i'_{\mu - 1} F_{i' - \mu + 1,n - i' - \lambda - 1 + \mu } + i'_\mu E_{i' - \mu ,n - i' - _\lambda + \mu } } \right)} \right\} = o. \hfill \\ \end{gathered} \) (n-i′) ist immer dann und nur dann von Null verschieden, wenn (λ+1−μ)≦(n−i′) ist; im Grenzfalle λ+1−λ=n−i′, bekommen wir O0=1 (No 6). Also erstreckt sich die Summation nach μ von λ+1−(n−i′) bis λ+1. Demnach können wir die frühere Gleichung folgendermassen schreiben:\(\begin{gathered} \mathop {\sum _\mu }\limits_{\lambda + 2 - \left( {\mu - i'} \right)}^{\lambda + 1} \left\{ {} \right\} + e_{\lambda ,\lambda + 1 - \left( {n - i'} \right)} \left( {2i'_{\lambda - \left( {n - i'} \right)} + i'_{\lambda + 1 - \left( {n - i'} \right)} } \right)E_{n - \lambda ,0} \hfill \\ + \bar e_{\lambda ,\lambda + 1 - \left( {n - i'} \right)} \left( {2i'_{\lambda - \left( {n - i'} \right)} F_{n - \lambda ,0} + i'_{\lambda + 1 - \left( {n - i'} \right)} E_{n - \lambda - 1 - 1} } \right) = o. \hfill \\ \end{gathered} \) Der Ausdrucki′ λ−(n−i′) verschwindet nur dann, wenni′−(n−λ)>i′, wenn alson−λ<0, was unmöglich ist; demnach kann weder der Coefficient vone λ,λ+1−(n−i′) noch der Coefficient von ēλλ+1-(n-i ′) verschwinden. Weil fernerE n−λ,0 undF n−λ,0 unter dem Summenzeichen nicht auftreten können, so erhält man:\(e_{\lambda ,\lambda + 1 - \left( {n - i'} \right)} = \bar e_{\lambda ,\lambda + 1 - \left( {n - i'} \right)} = o.\). Dieses Resultat gilt aber nur dann, wenn λ−(n−i′)≧0 ist; also ergiebt sich:\(e_{\lambda 1} = \bar e_{\lambda 1} = e_{\lambda 2} = \bar e_{\lambda 2} = \ldots = e_{\lambda ,\lambda + 1} = \bar e_{\lambda ,\lambda + 1} = o.\) (λ=0,1,...,n)Es handelt sich also nur darum, zu beweisen, dass\(e_{\lambda 0} = \bar e_{\lambda 0} = o\) (λ=0, 1, …,n) ist. Setzt man in der Identität (a)i′=μ=0, so ergiebt sich:\(e_{\lambda 0} n_{\lambda + 1} E_{1,n - \lambda - 1} + \bar e_{\lambda 0} n_{\lambda + 1} E_{0,n - \lambda } = o,\), wo wir mit dem Multiplicatorn λ+1 dividieren dürfen, ausser wenn λ=n ist, won λ+1=0 ist; wir erhalten also eλ0 = ēλ0 = 0 (λ=0, 1, …,n−1). Weil aber allee nμ und ēnμ gleich Null sein müssen, so erhalten wir:\(e_{\lambda 0} = \bar e_{\lambda 0} = o.\left( {\lambda = 0,1, \ldots n} \right)\) Damit ist aber unsere Behauptung bewiesen.
Die Gleichungen 1), 2), 3) haben 5 gemeinsame Lösungen:\(c_1 = \frac{{\varphi _{10} }}{{\sqrt E }},c_2 = \frac{{\varphi _{10} }}{{\sqrt E }},c_3 = \frac{{E\varphi _{01} - F\varphi _{10} }}{{\sqrt E \left( {EG - F^2 } \right)}},c_4 = \frac{{E\varphi _{01} - F\varphi _{10} }}{{\sqrt E \left( {EG - F^2 } \right)}},c_5 = \frac{{Fy' + E}}{{y'\sqrt {EG - F^2 } }}.\) Verfährt man, wie im Theorem V angedeutet ist, so erhält man aus 4) die Gleichung:\(c_3 \frac{{\partial f}}{{\partial c_1 }} + c_4 \frac{{\partial f}}{{\partial c_2 }} - c_1 \frac{{\partial f}}{{\partial c_3 }} - c_2 \frac{{\partial f}}{{\partial c_3 }} - c_2 \frac{{\partial f}}{{\partial c_4 }} + \left( {I + c_5^2 } \right)\frac{{\partial f}}{{\partial c_5 }} = o,\), welche schliesslich folgende 4 unabhängige Lösungen giebt:\(c_1^2 + c_3^2 = \Delta \varphi ,c_2^2 + c_4^2 = \Delta \psi ,c_1 c_2 + c_3 c_4 = \nabla \varphi \psi ,\frac{{c_3 + c_1 c_5 }}{{\sqrt {I + } c_5^2 }} = I\left( {\varphi y'} \right).\). (I(ϕy′)) ist keine neue Biegungsinvariante; man sieht leicht, dass sie mit dem Ausdrucke identisch ist, den HerrDarboux mit\(\frac{{\delta \varphi }}{{\delta s}}\) bezeichnet.Leçons sur la théorie générale des surfaces. Troisième partie, p. 195.)
Die Grössena, b, c sind Lösungen der Gleichungen der Classe 1 und ergeben sich ohne Schwierigkeit. Führt man diese Integralea, b, c in die Gleichungen 1), 2), 3), 4) ein, so erhält man das System:
 , Die Gleichungen 1), 2), 3) ergeben sehr leicht die Lösungen:\(\begin{gathered} \gamma _1 = \frac{{\varphi _{10} }}{{\sqrt E }},\gamma _2 = \frac{{E\varphi _{01} - F\varphi _{10} }}{{\sqrt {E\left( {EG - F^2 } \right)} }},\gamma _3 = \frac{{ac - b^2 }}{{\left( {EG - F^2 } \right)^3 }}, \hfill \\ \gamma _4 = \frac{a}{{E\left( {EG - F^2 } \right)}},\gamma _5 = \frac{{Eb - Fa}}{{E\left( {\sqrt {EG - F^2 } } \right)^3 }}; \hfill \\ \end{gathered} \) setzt man diese Lösungen in 4) ein, so findet man erstens, dass λ3=Δ
″2
eine Biegungsinvariante ist, zweitens die Gleichung:\(\gamma _2 \frac{{\partial f}}{{\partial \gamma _1 }} - \gamma _1 \frac{{\partial f}}{{\partial \gamma _2 }} + 2\gamma _5 \frac{{\partial f}}{{\partial \gamma _4 }} + \frac{I}{{\gamma _4 }}\left( {\gamma _3 + \gamma _3^2 - \gamma _4^2 } \right)\frac{{\partial f}}{{\partial \gamma _5 }} = o.\). Daraus ergiebt sich: 1) die Lösung: Δϕ=λ
12
+λ
22
;2 die Gleichung:\(2\gamma _5 \frac{{d\gamma _5 }}{{d\gamma _4 }} - \frac{{\gamma _3 + \gamma _5^2 }}{{\gamma _4 }} + \gamma _4 = o,\) welche sich vermöge der Substitution λ3+λ
35
=z auf eine lineare bringen lässt und die Lösung\(\Delta _2 \varphi = \frac{{\gamma _3 + \gamma _4^2 + \gamma _5^2 }}{{2\gamma _4 }}\) ergiebt, und endlich 3) die Gleichung:\(\frac{{2d\gamma _2 }}{{\sqrt {\Delta \varphi - \gamma _2^2 } }} + \frac{{d\gamma _4 }}{{\sqrt {\gamma _4 \left( {2\Delta _2 \varphi - \gamma _4 } \right) - \gamma _3 } }} = o,\) woraus wir die Biegungsinvariante Δ
′2
ϕ=2λ1λ2λ5+(λ
21
-λ
22
-)(λ4-Δ2ϕ) bekommen.
, Die Gleichungen 1), 2), 3) ergeben sehr leicht die Lösungen:\(\begin{gathered} \gamma _1 = \frac{{\varphi _{10} }}{{\sqrt E }},\gamma _2 = \frac{{E\varphi _{01} - F\varphi _{10} }}{{\sqrt {E\left( {EG - F^2 } \right)} }},\gamma _3 = \frac{{ac - b^2 }}{{\left( {EG - F^2 } \right)^3 }}, \hfill \\ \gamma _4 = \frac{a}{{E\left( {EG - F^2 } \right)}},\gamma _5 = \frac{{Eb - Fa}}{{E\left( {\sqrt {EG - F^2 } } \right)^3 }}; \hfill \\ \end{gathered} \) setzt man diese Lösungen in 4) ein, so findet man erstens, dass λ3=Δ
″2
eine Biegungsinvariante ist, zweitens die Gleichung:\(\gamma _2 \frac{{\partial f}}{{\partial \gamma _1 }} - \gamma _1 \frac{{\partial f}}{{\partial \gamma _2 }} + 2\gamma _5 \frac{{\partial f}}{{\partial \gamma _4 }} + \frac{I}{{\gamma _4 }}\left( {\gamma _3 + \gamma _3^2 - \gamma _4^2 } \right)\frac{{\partial f}}{{\partial \gamma _5 }} = o.\). Daraus ergiebt sich: 1) die Lösung: Δϕ=λ
12
+λ
22
;2 die Gleichung:\(2\gamma _5 \frac{{d\gamma _5 }}{{d\gamma _4 }} - \frac{{\gamma _3 + \gamma _5^2 }}{{\gamma _4 }} + \gamma _4 = o,\) welche sich vermöge der Substitution λ3+λ
35
=z auf eine lineare bringen lässt und die Lösung\(\Delta _2 \varphi = \frac{{\gamma _3 + \gamma _4^2 + \gamma _5^2 }}{{2\gamma _4 }}\) ergiebt, und endlich 3) die Gleichung:\(\frac{{2d\gamma _2 }}{{\sqrt {\Delta \varphi - \gamma _2^2 } }} + \frac{{d\gamma _4 }}{{\sqrt {\gamma _4 \left( {2\Delta _2 \varphi - \gamma _4 } \right) - \gamma _3 } }} = o,\) woraus wir die Biegungsinvariante Δ
′2
ϕ=2λ1λ2λ5+(λ
21
-λ
22
-)(λ4-Δ2ϕ) bekommen.Der Ausdruck, welcher in Klammern {} steht, ist die einzige gemeinsame Lösung der Gleichungen der Classe 1. Bezeichnet man diesen Ausdruck mitc und setzt man ihn in 1), 2), 3), 4) ein, so ergiebt sich das System:
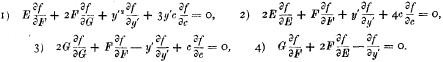 Die Gleichungen 1), 2), 3) ergeben zwei gemeinsame Lösungen:\(a = \frac{{E + Fy'}}{{y'\sqrt {EG - F^2 } }}\) und\(\beta = \frac{{cE^{{\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 2}}\right.\kern-\nulldelimiterspace}\!\lower0.7ex\hbox{$2$}}} }}{{y'\left( {EG - F^2 } \right)^2 }}\); demnach nimmt die Gleichung 4) die Form:\(\left( {I + \alpha ^2 } \right)\frac{{\partial f}}{{\partial \alpha }} + 3\alpha \beta \frac{{\partial f}}{{\partial \beta }} = o\) an und liefert das Integral\(C = \frac{\beta }{{\left( {I + \alpha ^2 } \right)^{{\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 2}}\right.\kern-\nulldelimiterspace}\!\lower0.7ex\hbox{$2$}}} }} = \frac{c}{{\sqrt {EG - F^2 \left( {E + 2Fy' + Gy'^2 } \right)^3 } }}.\)
Die Gleichungen 1), 2), 3) ergeben zwei gemeinsame Lösungen:\(a = \frac{{E + Fy'}}{{y'\sqrt {EG - F^2 } }}\) und\(\beta = \frac{{cE^{{\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 2}}\right.\kern-\nulldelimiterspace}\!\lower0.7ex\hbox{$2$}}} }}{{y'\left( {EG - F^2 } \right)^2 }}\); demnach nimmt die Gleichung 4) die Form:\(\left( {I + \alpha ^2 } \right)\frac{{\partial f}}{{\partial \alpha }} + 3\alpha \beta \frac{{\partial f}}{{\partial \beta }} = o\) an und liefert das Integral\(C = \frac{\beta }{{\left( {I + \alpha ^2 } \right)^{{\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 2}}\right.\kern-\nulldelimiterspace}\!\lower0.7ex\hbox{$2$}}} }} = \frac{c}{{\sqrt {EG - F^2 \left( {E + 2Fy' + Gy'^2 } \right)^3 } }}.\)
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Żorawski, K. Über Biegungsinvarianten. Acta Math. 16, 1 (1892). https://doi.org/10.1007/BF02418986
DOI: https://doi.org/10.1007/BF02418986


 , Die Gleichungen 1), 2), 3) ergeben sehr leicht die Lösungen:
, Die Gleichungen 1), 2), 3) ergeben sehr leicht die Lösungen: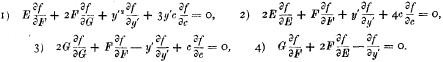 Die Gleichungen 1), 2), 3) ergeben zwei gemeinsame Lösungen:
Die Gleichungen 1), 2), 3) ergeben zwei gemeinsame Lösungen: