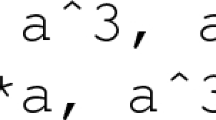Abstract
A theorem of inertness for a class of semigroup rings is proved. An example showing that this class of rings is not totally inert is constructed.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
Literature cited
G. M. Bergman, “Centralizers in free associative algebras,” Trans. Am. Math. Soc.,137, 327–344 (1969).
B. V. Tarasov, “On free associative algebra,” Algebra Logika,6, No. 4, 93–105 (1967).
P. M. Cohn, Free Rings and Their Relations, Academic Press, London-New York (1971).
L. A. Bokut', “Factorization theorems for certain classes of rings without zero divisors, I,” Algebra Logika,4, No. 4, 25–52 (1965).
L. A. Bokut', “Some examples of rings without zero divisors,” Algebra Logika,3, Nos. 5–6, 5–28 (1964).
é. G. Koshevoi, “On serving subalgebras of free associative algebras,” Algebra Logika,10, No. 2, 183–187 (1971).
Additional information
Translated from Matematicheskie Zametki, Vol. 22, No. 3, pp. 453–463, September, 1977.
The author thanks L. A. Bokut' for assistance with the article.
Rights and permissions
About this article
Cite this article
Tarasov, B.V. A class of inert semigroup rings. Mathematical Notes of the Academy of Sciences of the USSR 22, 742–748 (1977). https://doi.org/10.1007/BF02412506
Received:
Issue Date:
DOI: https://doi.org/10.1007/BF02412506