Abstract
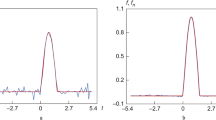
The article considers the construction of a stable approximation of the basic component in an experimental spectrum. Conditions of independence and nondegeneracy are introduced for the local resonance nonhomogeneities and the basic component, which is treated as a continuous smooth function whose local variation is substantially less than the variation of the local nonhomogeneities. The problem of approximating the basic component is shown to have a unique solution under these conditions. A stable algorithm is developed for the construction of the basic component. The algorithm is applied to construct the basic component from typical spectrometric data, and the results are compared with other known basic-component fitting methods.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
R. G. Helmer and M. A. Lee, “Analytical functions for fitting peaks from Ge semiconductor detetors,” Nucl. Instr. Meth.,178, 499–512 (1980).
M. Acena and E. Garcia-Torano, “Method to fit alpha spectra,” Nucl. Instr. Meth.,123, 346–348 (1984).
A. N. Tikhonov and V. Ya. Arsenin, Methods of Solution of Ill-Posed Problems [in Russian], Nauka, Moscow (1986).
A. N. Tikhonov et al. (eds.), Regularizing Algorithms and Prior Information [in Russian], Nauka, Moscow (1983).
P. N. Zaikin and E. Yu. Shchetinin, “A stable algorithm for reconstruction of the basic component of an experimental spectrum” in: Mathematical Modeling and Solution of Inverse Problems of Mathematical Physics [in Russian], Izd. MGU, Moscow (1994), pp. 76–82.
V. V. Voevodin and Yu. A Kuznetsov, Matrices and Computation [in Russian], Moscow (1984).
P. N. Zaikin and E. Yu. Shchetinin, A Method of Solving the Problem of Localization of Positions of Resonance Nonhomogeneities [in Russian], Unpublished manuscript, VINITI RAN 841-V93/2.04.93 (1993).
A. B. Bakushinskii and A. V. Goncharskii Ill-Posed Problems: Numerical Methods and Applications [in Russian], Izd. MGU, Moscow (1989).
P. N. Zaikin and M. V. Ufimtsev, Methods and Data for Computer-Aided Processing of Experimental Results [in Russian], Izd. MGU, Moscow (1987).
A. N. Tikhonov (ed.), A Library of Programs for Processing and Interpretation of Experimental Results [in Russian], Izd. MGU, Moscow (1988).
D. Rockafellar, Convex Analysis [Russian translation], Mir, Moscow (1973).
P. N. Zaikin and N. D. Ogorodnikova, “An efficient numerical algorithm for constructing the background component in spectrometry,” in: Mathematical Problems of Experimental Analysis [in Russian], Izd. MGU, Moscow (1984), p. 44–48.
P. Paatero, The Extreme Value Estimation Deconvolution Method with Applications in Aerosol Research, Report Series in Physics HU-P-250, Univ. of Helsinki (1990).
Additional information
Translated from Chislennye Metody v Matematicheskoi Fizike, Published by Moscow University, Moscow, 1996, pp. 137–146.
Rights and permissions
About this article
Cite this article
Zaikin, P.N., Shchetinin, E.Y. A method for approximate construction of the basic component in the class of functions of bounded variation. Comput Math Model 8, 172–180 (1997). https://doi.org/10.1007/BF02405169
Issue Date:
DOI: https://doi.org/10.1007/BF02405169