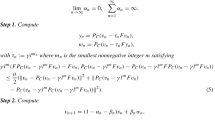Conclusion
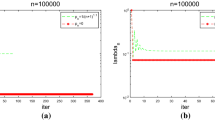
In the optimization problem [f 0(x)│hi(x)<-0,i=1,…,l] relaxation of the functionf 0(x)+Nh+(x) does not produce, as we know [6, 7], αk=1 in Newton's method with the auxiliary problem (5), (6), whereF(x)=f 0′(x). For this reason, Newton type methods based on relaxation off 0(x)+Nh+(x) are not superlinearly convergent (so-called Maratos effect). The results of this article indicate that if (F(x)=f 0′(x), then replacement of the initial optimization problem with a larger equivalent problem (7) eliminates the Maratos effect in the proposed quasi-Newton method. This result is mainly of theoretical interest, because Newton type optimization methods in the space of the variablesx ∈R n are less complex. However to the best of our knowledge, the difficulties with nonlocal convergence arising in these methods (choice of parameters, etc.) have not been fully resolved [10, 11]. The discussion of these difficulties and comparison with the proposed method fall outside the scope of the present article, which focuses on solution of variational inequalities (1), (2) for the general caseF′(x)≠F′ T(x).
Similar content being viewed by others
References
P. t. Harker and J. S. Pang, “Finite-dimensional variational inequality and nonlinear complementarity problems: a survey of theory, algorithms and applications”, Math. Progr., Ser. B,48, No. 2, 161–220 (1990).
B. N. Pshenichnyi and M. U. Kalzhanov, “A method for solving variational inequalities”, Kibern. Sistem. Anal., No. 6, 48–55 (1992).
E. N. Khobotov, “A modification of the extragradient method for solving variational inequalities and some optimization problems. Zh. Vychisl. Matem. Mat. Fiziki,27, No. 10, 1462–1473 (1978).
Ya. M. Bakushinskii and B. T. Polyak, “Solving variational inequalities”, Dokl. Akad. Nauk SSSR,219, No. 5, 1038–1041 (1974).
V. M. Panin and V. M. Aleksandrova, “Linear convergence of a method for solving variational inequalities”, Kibern. Sistem. Anal., No. 3, 175–179 (1994).
D. Bertsekas, Constrained Optimization and Lagrange Multiplier Methods, Academic Press, New York (1982).
V. M. Panin, “Finite penalty methods with linear approximation of constraints, II”, Kibernetika, No. 4, 73–81 (1984).
V. M. Panin, “Finite Penalty Methods in Nonlinear Constrained Optimization [in Russian], Thesis, Kiev (1989).
V. M. Panin, “On some methods for solving convex programming problems”, Zh. Vychisl. Matem. Mat. Fiziki,21, No. 2, 315–328 (1981).
Yu. M. Danillin, “Sequential quadratic programming methods with step control using the Lagrange function”, Kibern. Sistem. Anal., No. 3, 70–77 (1994).
Yu. M. Danilin, “Sequential quadratic programming and augmented Lagrange functions”, Kibern. Sistem. Anal., No. 3 (1994).
Additional information
Translated from Kibernetika i Sistemnyi Analiz, No. 6, pp. 78–91, November–December, 1994.
Rights and permissions
About this article
Cite this article
Panin, V.M., Aleksandrova, V.M. Nonlocal quasi-Newton method for solving convex variational inequalities. Cybern Syst Anal 30, 855–865 (1994). https://doi.org/10.1007/BF02366444
Received:
Issue Date:
DOI: https://doi.org/10.1007/BF02366444