Skip to main content
SpringerLink
Log in

Acoustic diffraction by two concentric coaxial soft spherical caps

  • Published:
Journal of Engineering Mathematics Aims and scope Submit manuscript

Summary

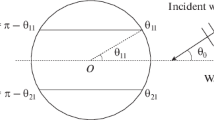
The subject of this paper is the problem of diffraction of a time-harmonic axially symmetric acoustic wave by two concentric coaxial soft spherical caps. An integral equation technique is employed to solve such a boundary value problem involving two concentric coaxial spherical caps. Approximate expressions are derived for the far field amplitude as well as the scattering cross section for this problem when the incident wave is a low frequency axially symmetric plane wave travelling along the common axis of the two caps. By taking appropriate limits, the formulae for scattering cross section for the corresponding problems for a soft spherical cap, a soft sphere and a soft sphere bounded by a concentric soft spherical cap are also derived. Furthermore, the total electrostatic charge required to raise the two concentric coaxial spherical caps to unit potentials in a free space is readily evaluated from the analysis of this paper.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. W. D. Collins, Some scalar diffraction problems by a spherical cap,Arch. Rat. Mech., Analys., 10 (1962) 249–266.

    MATH  Google Scholar 

  2. D. P. Thomas, Diffraction by a spherical cap,Proc. Camb. Phil. Soc., 59 (1963) 197–209.

    MATH  Google Scholar 

  3. D. L. Jain and R. P. Kanwal, An integral equation perturbation technique in applied mathematics,J. Applicable, Analys., to appear.

  4. D. L. Jain and R. P. Kanwal, Acoustic diffraction by a perfectly soft annular spherical capInt. J. Engng. Sc. 10 (1972) 193–211.

    Google Scholar 

  5. D. L. Jain and R. P. Kanwal, Acoustic diffraction by a rigid annular spherical cap,J. Appl. Mech. 39, Series E Mechanics (1972), 139–147.

    Google Scholar 

  6. W. D. Collins, Some scalar diffraction problems for circular disks,Quart. J. Mech. Appl. Math., 14 (1961) 101–117.

    MATH  MathSciNet  Google Scholar 

  7. B. K. Vaid and D. L. Jain, Acoustic diffraction by two coaxial soft and rigid circular disks, to appear.

  8. B. K. Vaid and D. L. Jain, An integral equation technique,SIAM, J., Appl. Math. 26 (1974), to appear.

  9. R. P. KanwalLinear integral equations, theory and technique, Academic Press, New York (1971).

    Google Scholar 

  10. W. Magnus and F. Oberhettinger,Formulas and theorems for the special functions of mathematical, physics, Springer Publishing House (1943).

  11. I. N. Sneddon,Mixed boundary value problems in potential theory, John Wiley and Sons, Inc., (1966), New York.

  12. B. K. Vaid and D. L. Jain,Some electrostatic and hydrodynamic problems for two spherical caps, to appear.

Download references

Author information

Authors and Affiliations

  1. Faculty of Mathematics, University of Delhi, Delhi-7, India

    B. K. Vaid & D. L. Jain

Authors
  1. B. K. Vaid
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. D. L. Jain
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Vaid, B.K., Jain, D.L. Acoustic diffraction by two concentric coaxial soft spherical caps. J Eng Math 8, 81–88 (1974). https://doi.org/10.1007/BF02353608

Download citation

  • Received:

  • Revised:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF02353608

Keywords

Search

Navigation