Abstract
Biaxial tensile experiments with thin rubber sheets, containing an internal crack, reveal the possibility to simulate and readily check the exact linear-elastic crack-flank displacements. The resulting deformed shape and the final position during loading of an internal inclined crack in an infinite, biaxially loaded elastic plate, was defined by measuring the crack-flank displacements, and the deformation features of the internal crack in rubber sheets. The results were compared with the linear-elastic displacements and the respective features, which have been obtained from an infinitesimal elasticity theory.
The calculation of these displacement and deformation properties for a given crack presupposes the determination of two parameters, which characterize the loading conditions of the boundaries of the elastic cracked plate. These parameters have been determined as Lagrangian or Eulerian ones from the homogeneous strains at the boundaries of the elastic sheet, assuming either a Hookean, or a neo-Hookean or a Mooney material behavior for the elastic sheet.
It has been shown that, except for the vicinities of the crack tips and for the regions of the imposed boundary strains in the experiments, the observed crack-flank displacements agree satisfactorily with the respective displacements obtained from the infinitesimal theory, if the material behavior is assumed as a neo-Hookean one, and the boundary-loading parameters are calculated as Eulerian ones.
Similar content being viewed by others
Abbreviations
- a :
-
half-crack length
- a 1,a 2 :
-
lengths of the major and minor semiaxes of the deformed crack
- c :
-
loading parameter
- C 1,C 2 :
-
material constants (rubber elasticity)
- E :
-
modulus of elasticity
- E:
-
upper index defining Eulerian values of a quantity
- f 1,f 2,f 0 :
-
Lagrangian stresses
- H:
-
lower index defining values of a quantity for Hookean material behavior
- I 1,I 2,I 3 :
-
strain invariants
- k :
-
biaxiality factor
- L:
-
upper index defining Lagrangian values of a quantity
- M:
-
lower index defining values of a quantity for Mooney material behavior
- N:
-
lower index defining values of a quantity for neo-Hookean material behavior
- t 1,t 2 :
-
Eulerian stresses
- u ± :
-
upper and lower crack-flank displacement in the x direction
- v ± :
-
upper and lower crack-flank displacement in the y direction
- W :
-
strain-energy-density function
- β:
-
angle of inclination of the initial crack
- ɛ1,ɛ2 :
-
principal strains (linear elasticity)
- θ:
-
angular displacement of the deformed crack
- λ:
-
angular displacement of the effective crack axis
- λ1,λ2,λ3 :
-
principal extension ratios (biaxial)
- λo :
-
extension ratio (simple extension)
- ν:
-
Poisson's ratio
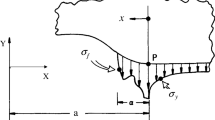
- σ1,σ2 :
-
principal stresses at infinity (linear elasticity)
References
Theocaris, P.S., Pazis, D. andKonstantellos, B.D., “The Exact Shape of a Deformed Internal Slant Crack Under Biaxial Loading,”Int. J. Fract.,30,135–153 (1986).
Theocaris, P.S., “The Exact Form and Properties of the Deformed Transverse Internal Elastic Crack,”Eng. Fract. Mech.,23,851–862 (1986).
Theocaris, P.S., “Displacement Constraints of the Faces of Internal Cracks Due to Pure Shear,”Eng. Fract. Mech.,24,383–397 (1986).
Theocaris, P.S., “Paradoxes in the Deformation Modes of Crack Flanks Due to Shear,”Eng. Fract. Mech.,26,251–266 (1986).
Theocaris, P.S., “K III-Deformation Modes in Internal Oblique Cracks Under Plane-Stress Conditions,”Experimental Mechanics,27 (2),220–228 (1987).
Theocaris, P.S., “The Internal Crack in an Extended or Compressed Plate: Its Geometric Characteristics,”Eng. Fract. Mech.,26,753–770 (1986).
Pazis, D., Theocaris, P.S. andKonstantellos, B.D., “Elastic Overlapping of the Crack Flanks Under Mixed-Mode Loading,”Int. J. Fract.,37,303–319 (1988).
Theocaris, P.S., “In-Plane Stresses and Strains Along the Flanks of an Internal Elastic Crack,”Eng. Fract. Mech.,30 (2),145–159 (1988).
Andrews, E.H., “Stresses at a Crack in an Elastomer,”Proc. Phys. Soc.,17,483–498 (1961).
Knauss, W.G., “Stresses Near a Crack in a Rubber Sheet,”Experimental Mechanics,25,177–181 (1968).
Green, A.E. andAdkins, J.E., Large Elastic Deformations, Clarendon Press, Oxford (1970).
Green, A.E. andZerna, W., Theoretical Elasticity, Clarendon Press, Oxford (1954).
Treloar, L.R.G., The Physics of Rubber Elasticity, Clarendon Press, Oxford (1958).
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Theocaris, P.S., Pazis, D. & Konstantellos, B.D. Elastic displacements along the flanks of internal cracks in rubber. Experimental Mechanics 29, 32–39 (1989). https://doi.org/10.1007/BF02327778
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1007/BF02327778