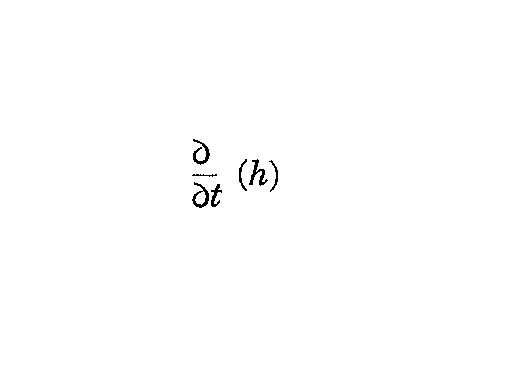Skip to main content
SpringerLink
Log in

Design considerations and analysis of a complex-modulus apparatus

Equipment has been designed to measure the dynamic properties of viscoelastic materials in shear. Measurements taken with this equipment indicate that the experimental difficulties are not extensive and the results are reliable and consistent

  • Published:
Experimental Mechanics Aims and scope Submit manuscript

Abstract

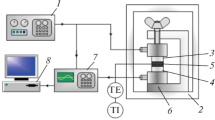
An analytical assessment is made of an apparatus designed for the measurement of the complex shear modulus of viscoelastic materials. It is shown that simple measurements of amplitude ratio and phase angle are sufficient to determine the complex modulus at any point over a wide range of frequency and dynamic strain. Data obtained for butyl rubber and some experimental elastomers are presented.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Abbreviations

A :

specimen area

b :

specimen thickness

c :

velocity of shear waves in an elastic\(material = \sqrt {G/_\rho } \)

f :

the frequency of vibration

G :

elastic shear modulus

G * :

complex shear modulus=G′+iG″=G 0 exp (iθ)

G′:

storage modulus in shear=G 0 cos θ

G″:

loss modulus in shear=G 0 sin θ

G 0 :

magnitude of the complex shear modulus

θ:

loss angle in shear=arc tan (G″/G′)

i :

\(\sqrt { - 1} \)

Q :

displacement amplitude of lower block

\(\bar Q\) :

displacement amplitude of upper block or free mass

R :

ratio,\(\bar Q/Q\)

u :

displacement in thex direction

W :

weight of the free mass, the center of gravity of which is at the top of the specimen

x, y :

rectangular coordinate axes

ω:

circular frequency=2πf

ϕ:

phase angle between the lower and upper blocks

τ:

shear stress

ϱ:

mass density of the specimen material

\(\dot h\) :
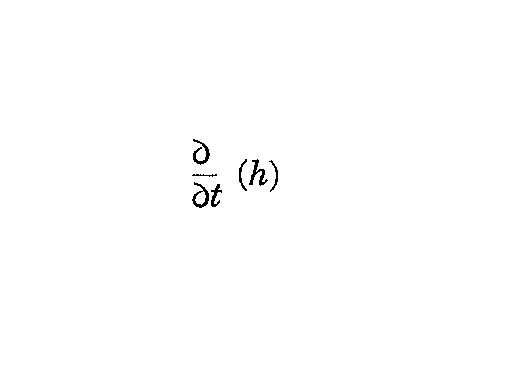
figure 1
H :

\(\left( {\omega ^2 Mb} \right)/A\)

g :

acceleration of gravity=386 in./sec2

k :

\(\frac{\omega }{c} = \frac{\omega }{{\sqrt {G/\rho } }}\)

k * :

\(\frac{\omega }{{\sqrt {G^* /\rho } }}\)

References

  1. Snowdon, J. C., “Representation of the Mechanical Damping Possessed by Rubberlike Materials and Structures,”Jnl. ASA,35 (6),821–829 (June1963).

    Google Scholar 

  2. Gross, B., Mathematical Structure of the Theories of Viscoelasticity, Hermann and Company, Paris (1953).

    Google Scholar 

  3. Read, W. T., “Effect of Stress-Free Edges in Plane Shear of a Flat Body,”Jnl. Appl. Mech.,17,349–352 (December1960).

    Google Scholar 

  4. Alfrey, T., Jr., “Non-Homogeneous Stresses in Viscoelastic Media,”Quart. Appl. Math.,2,113–119 (July1944).

    MATH  MathSciNet  Google Scholar 

  5. Lee, E. H., “Stress Analysis in Viscoelastic Bodies,”,13,183–190 (July1955).

    MATH  MathSciNet  Google Scholar 

  6. Read, W. T., “Stress Analysis for Compressible Viscoelastic Materials,”Jnl. Appl. Phys.,21,671–674 (July1950).

    MATH  MathSciNet  Google Scholar 

  7. Berry, D. S., “Stress Propagation in Viscoelastic Bodies,”Jnl. Mech. Phys. Solids,6,177–185 (1958).

    MATH  MathSciNet  Google Scholar 

  8. Maxwell, B., “An Apparatus for Measuring the Response of Polymeric Materials to an Oscillating Strain,”ASTM Bltn. No. 215, 76, (July1956).

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Metals and Ceramics Division, Air Force Materials Laboratory, Wright-Patterson Air Force Base, Ohio

    Richard L. Adkins

  2. Research and Technology Division, Air Force Systems Command, Wright-Patterson Air Force Base, Ohio

    Richard L. Adkins

Authors
  1. Richard L. Adkins
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Adkins, R.L. Design considerations and analysis of a complex-modulus apparatus. Experimental Mechanics 6, 362–367 (1966). https://doi.org/10.1007/BF02327213

Download citation

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF02327213

Keywords

Search

Navigation