Abstract
For a unidirectional lamina, the in-plane mechanical properties of interest areE 11,E 22, ν12, ν12 andG 12. Only three of the first four listed are independent. The fourth may be calculated from the reciprocal relationshipE 11 ν21 =E 22 ν12, which results from stiffness-tensor symmetry. Measurement of any four of the five properties listed will completely characterize the in-plane mechanical properties. A longitudinal uniaxial tension test was used to evaluate longitudinal modulus and Poisson's ratio. A modified rail-shear apparatus was designed to measure shear modulus in a rail-shear orientation, as well as a totally constrained transverse modulus in a uniaxial tension test with an orientation transverse to the longest dimension of the specimen. A flexure test was also used to estimate transverse moduli, since the achievement of the totally constrained transverse-modulus measurement was impaired by the variability of load distribution and constraint across the breadth (10-in. length) of the specimen. An apparatus was designed that applied a line loading to the specimen, simply supported on two opposite sides, with the two remaining sides free. The feasibility of this technique was documented by comparing measured values of the transverse modulus and out-of-plane displacement for a [0°]4 specimen to values obtained from the Levy solution for bending of an orthotropic plate.
Similar content being viewed by others
Abbreviations
- a :
-
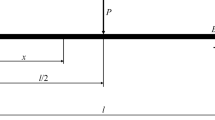
specimen length, in. (mm)
- b :
-
distance between parallel simple supports, in. (mm)
- E 11 :
-
stiffness parallel to the fiber direction in Msi (millions of pounds/square inch) or GPa
- \(\bar E_{11} \) :
-
constrained modulus parallel to the fiber direction, Msi (GPa)
- E 22 :
-
stiffness transverse to the fiber direction, Msi (GPa)
- \(\bar E_{22} \) :
-
constrained modulus transverse to the fiber direction, Msi (GPa)
- G 12 :
-
in-plane shear modulus in terms of material coordinates, Msi (GPa)
- \(\bar P\) :
-
magnitude of linearly distributed loading, lb/in. (N/m)
- Q 11,Q 22,Q 12,Q 66 :
-
reduced in-plane stiffnesses, Msi (GPa)
- ν:
-
distance from simple support to applied linear distributed loading, in. (mm)
- w :
-
out-of-plane displacement, in. (mm)
- γ12 :
-
in-plane engineering shear strain in terms of material coordinates
- ∈1 :
-
strain parallel to the fiber direction
- ∈2 :
-
strain transverse to the fiber direction
- ∈45 :
-
strain measured at 45 deg to the load axis
- ∈ x :
-
strain in direction parallel to load axis
- ∈ y :
-
strain in a direction perpendicular to load axis
- ν12 :
-
Poisson's ratio for transverse strain in the 2 direction when stressed in the 1 direction
- ν21 :
-
Poisson's ratio for transverse strain in the 1 direction when stressed in the 2 direction
- σ1 :
-
normal stress parallel to the fiber direction, Ksi (MPa)
- σ2 :
-
normal stress transverse to the fiber direction, Ksi (MPa)
- τ12 :
-
in-plane shear stress in terms of material coordinates, Ksi (MPa)
References
Chang, F.H., Gordon, D.E., Rodini, B.T. and McDaniel, R.H., “Real-time Characterization of Damage Growth in Graphite-Epoxy Laminates,” J. Comp. Mat.,10 (July 1976).
Chang, F.H., Gordon, D.E. and Gardner, A.H., “A Study of Fatigue Damage in Composites by Nondestructive Testing Techniques,” Fatigue of Filamentary Composite Materials, ASTM STP 636, K.L. Reifsnider and K.N. Lauraitis, Eds., Amer. Soc. for Test. and Mat. (1977).
Reifsnider, K.L., Stinchcomb, W.W. and O'Brien, T.K., “Frequency Effects on a Stiffness-Based Fatigue Failure Criterion in Flawed Composite Specimens,” Fatigue of Filamentary Composite Materials, ASTM STF 636, K.L. Reifsnider and K.N. Lauraitis, Eds., Amer. Soc. for Test. and Mat. (1977).
Waddoups, M.E., Eisenmann, J.R. and Kaminski, B.E., “Macroscopic Fracture Mechanics of Advanced Composite Materials,” J. Comp. Mat.,5, (Oct. 1971).
O'Brien, T.K. and Reifsnider, K.L., “Fatigue Damage: Stiffness/Strength Comparisons for Composite Materials,” J. of Test. and Eval.,5 (5) (1977).
Salkind, M.J., “Early Detection of Fatigue Damage in Composite Materials.” Paper #75-772, 16th AIAA, ASME, SAE Structures, Structural Dynamics, and Materials Conference, Denver, CO (May 1975).
O'Brien, T.K., “Effect of Gage Section Size on Composite Stiffness Measurements,” Comp. Tech. Rev.,1, (4) (Summer 1979).
Ashton, J.E. andWhitney, J.M., Theory of Laminated Plates, Technomic Publishers, Stamford, CT (1970).
Author information
Authors and Affiliations
Additional information
formerly Research Associate, Engineering Science and Mechanics Department, Virginia Polytechnic Institute and State University
Rights and permissions
About this article
Cite this article
O'Brien, T.K., Reifsnider, K.L. A complete mechanical-property characterization of a single composite specimen. Experimental Mechanics 20, 145–152 (1980). https://doi.org/10.1007/BF02327117
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF02327117