Skip to main content
SpringerLink
Log in

An analytical and experimental stress analysis of a practical mode II fracture test specimen

A boundary-collocation analysis employing the complete Williams stress function is applied in connjunction with a photoelastic experiment to determine crak-tip stress-intensity factors for a practical Mode II fracture test specimen

  • Published:
Experimental Mechanics Aims and scope Submit manuscript

Abstract

A boundary-collocation method has been employed to determine the Mode II stress-intensity factors for a pair of through-the-thickness edge cracks in a finite isotropic plate. An elastostatic analysis has been carried out in terms of the complete Williams stress function employing both even and old components. The results of the numerical analysis were verified by a two-step procedure whereby the symmetric (Mode I) and antisymmetric (Mode II) portions of the solution were independently compared with existing solutions. Since no previous analytical solutions existed for the asymmetric loading of an edge-cracked plate, the complete solution was verified by comparison with a photoelastic analysis.

A compact shear (CS) specimen of Hysol epoxy resin was loaded in a photoelastic experiment designed to study the isochromatic-fringe patterns resulting from the Mode II crack-tip stress distribution. The experiment verified that a pure mode II stress distribution existed in the neighborhood of the crack tips, and confirmed the accuracy of the boundary-collocation solution for the Mode II stress-intensity factors. Specimen center-line stress-distribution data were obtained photoelastically and employed to refine the boundary-collocation analysis. Agreement between the analytically and experimentally determined Mode II stress-intensity factors was excellent.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Abbreviations

a :

notch depth, cm

B 2,n ,C 2,n :

coefficients of the even stressfunction (opening mode) series associated with thenth eigenvalue

B 4,n ,C 4,n :

coefficients of the odd (sliding-mode stress-function series associated with thenth eigen-value

b, B :

specimen thickness, cm

E :

modulus of elasticity, Pa

f :

nondimensinoalized stress-intensity factorK II/σa 1/2

F σ :

material fringe constant, N/fr-m

h, H :

compact-shear-specimen quarter-width, cm

K,K I,K II,K III :

stress-intensity factor at the crack tip, subscript refers to mode of crack extension, Pa m1/2

K I c,K II c,K III c :

critical value of stress-intensity factor at point of instability of crack extension, Pa m1/2

m :

m-th term in eigenfunction expansion

N, n :

refers to thenth eigenvalue of the series expansion for the stress function-number of boundary stations; also refers to fringe order

\(\bar n\) :

refers to the outward unit normal vector drawn on the specimne boundary

P :

applied load; also total (elastic and plastic) work required to extend a crack, N

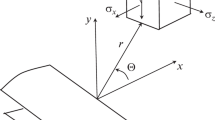
r, θ:

polar-coordinate directions with origin located at crack tip

t :

symbol for specimen thickness (photoelastic analysis), cm

w :

specimen length (for compact shear specimens) specimen width (for compact tension specimens)

X, Y, Z, x, y, z :

cartesian-coordinate directions

λ n :

nth eigenvalue for the Williams stress function

σ:

boundary stresses applied to compact shear specimens and compact tension specimen =P/BH, Pa

σ c :

critical fracture stress, Pa

σ r , σθ, σ z , τ r θ:

components of the stress tensor in polar coordinates, Pa

σ x , σ y , σ z :

components of the stress tensor, cartesian coordinates, Pa

σ ys :

tensile yield stress, Pa

σ 1 , σ 2 :

principal stresses, Pa

τ:

shear stress applied to tangs of compact shear specimen =KP/BH, Pa

τ m :

maximum in-plane shear stress, Pa

X :

Williams stress function (x=x I+x II), N

X I :

stress function for the stress-free (or zero-displacement) crack surface, N

X IE :

even stress-function component ofX I, N

X IO :

odd stress-function component ofX I, N

References

  1. Chisholm, D. B., “Dynamic Testing of Luminaire Supports,” Federal Highway Admin. Rep., FHWA RD 73-55, Washington, DC (July, 1973).

  2. Kobayashi, A. S., Wade, B. G., Bradley, W. B. andChiu, S. T., “Crack Branching in Homalite-100 Sheets,”Engrg. Fract. Mech.,6,81–92 (1974).

    Google Scholar 

  3. Inglis, C. E., Trans. Inst. Naval Architects,1 (1913).

  4. Griffith, A. A., Phil. Trans. Royal Soc. A221, 163–198 (1921).

    Google Scholar 

  5. Irwin, G. R., Fracture, Handbüch der Physik (Ed. S. Flügge),6, Elasticity and Plasticity, Springer, Berlin, 551–590 (1958).

    Google Scholar 

  6. Westergaard, H. M., “Bearing Pressures and Cracks,”Transact. of the ASME, J. of Ap. Mech.,61,A 49–53 (1930).

    Google Scholar 

  7. Sneddon, I. N., “The Distribution of Stress in the Neighborhood of a Crack in an Elastic Solid,”Proc. of the Royal Society, A 197, 229–260 (1946).

    Google Scholar 

  8. Williams, M. L., “On the Stress Distribution at the Base of a Stationary Crack,”Transact. of the ASME,79,109–114 (1957).

    Google Scholar 

  9. Erdogan, F., andSih, G. C., “On the Crack Extension in Plates Under Plane Loading and Transverse Shear,”Transact. of the ASME, J. of Basic Engrg.,85,519–527 (1963).

    Google Scholar 

  10. Wu, E. M. C., “A Fracture Criterion for Orthotropic Plates Under the Influence of Compression and Shear,” PhD Thesis, Univ. of Illinois (1965).

  11. Sawyer, S. G., “A Stress Intensity Factor Approach to the Analysis of Interfacial Cracks In Fiber Reinforced Composite Materials,” PhD Thesis, Carnegie-Mellon University (1969).

  12. Gross, B., “Some Plane Problem Elastostatic Solutions for Plates Having a V-Notch,” PhD Thesis, Case-Western Reserve Univ. (1970).

  13. Gyekenyesi, G. S., “Elastostatic Stress Analysis of Finite Anisotropic Plates with Centrally Located Traction Free Craks,” PhD Thesis, Michigan State, University (1972).

  14. Wilson, W. K., “On Combined Mode Fracture Mechanics,”Research Rep. 69-FMECH-RI, Westinghouse Research Labs, Pittsburgh, PA (June1969).

    Google Scholar 

  15. Shih, C. F., “Small-Scale Yielding Analysis of Mixed Mode Plane-Strain rack Problems,”Fracture Analysis, Proc. of the 1973 Nat. Symp. on Fract. Mech., Part II, ASTM STP 560, 187–210 (1974).

    Google Scholar 

  16. Chisholm, D. B., “An Elastostatic Analysis of the Second Fracture Mode,” Progress Reports 4 and 5 covering research conducted during the period of August-November 1973, submitted to the Director, Office of Personnel and Training, Federal Highway Administration, Washington, D.C.

  17. Jones, D. L. andChisholm, D. B., “An Investigation of the Edge-Sliding Mode in Fracture Mechanics,”Engrg. Fract. Mech.,7,261–270 (1975).

    Google Scholar 

  18. Chisholm, D. B. and Jones, D. L., “Determination of Critical Mode II Stress Intensity Factors for A533 B Steetl,” Proc. of the Eleventh Anntal Meeting of the Soc. of Engrg. Sci., Durham, NC (Nov. 1974).

  19. Chisholm, D. B., “An Analytical and Experimental Investigation of the Edge-Sliding Mode in Fracture Mechanics,”D.Sc. Dissertation, The George Washington University, Washington, D.C. (Feb.1975).

    Google Scholar 

  20. Smith, D. G. andSmith, C. W., “Photoelastic Determination of Mixed Mode Stress Intensity Factors,”Engrg. Fract. Mech.,4,357–366 (1972).

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Federal Highway Administration, 20590 HRS-12, Washington, DC

    D. B. Chisholm

  2. School of Engineering and Applied Science, The George Washington University, 20052, Washington, DC

    D. L. Jones (Associate Research Professor)

Authors
  1. D. B. Chisholm
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. D. L. Jones
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Chisholm, D.B., Jones, D.L. An analytical and experimental stress analysis of a practical mode II fracture test specimen. Experimental Mechanics 17, 7–13 (1977). https://doi.org/10.1007/BF02324265

Download citation

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF02324265

Keywords

Search

Navigation