Abstract
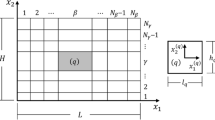
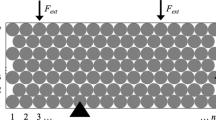
Three-point bending is simulated by an elaborate numerical procedure based on an elastoplastic, large deflection, contact analysis. A minimization formulation is used, which is equivalent to the incremental form posed as partial differential equations with inequalities. A sequential quadratic programming approach based on the finite-element technique is adopted as a method of solution. To examine the validity of the simulation method, experiments are carried out for specimens that have various widths.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
West, D.C., “Flexure Testing of Plastics,”Experimental Mechanics,4 (2),185–190 (1964).
Theocaris, P.S., Paipetis, S.A. andPaolinelis, S.G., “Three-point Bending at Large Deflections,”J. Test. and Eval.,5,427–436 (1977).
Paolinelis, S.G., Paipetis, S.A. andTheocaris, P.S., “Three-point Bending at Large Deflections of Beams with Different Moduli of Elasticity in Tension and Compression,”J. Test. and Eval.,7,177–182 (1979).
Panagiotopoulos, P.D., Inequality Problems in Mechanics and Applications; Convex and Non-convex Energy Functions, Birkhauser, Chapt. 9–11 (1985).
Standard Test Methods for Flexural Properties of Plastic and Electrical Insulating Materials, ASTM D790-71.
Chan, S.K. andTuba, I.S., “A Finite Element Method for Contact Problems of Solid Bodies, Part I. Theory and Validation,”Int. J. Mech. Sci.,13,627–639 (1971).
Francavilla, A. andZienkiewicz, O.C., “A Note on Numerical Computation of Elastic Contact Problems,”J. Num. Meth. Eng.,14,337–357 (1979).
Chand, R., Haug, E.J. andRim, K., “Analysis of Unbonded Contact Problems by Means of Quadratic Programming,”J. Optimization Theory and Application,20,171–189 (1976).
Cheng, J.H. andKikuchi, N., “An Analysis of Metal Forming Processes Using Large Deformation Elastic-plastic Formulations,”Comput. Meth. Appl. Mech. Eng.,49,71–108 (1985).
Bathe, K.J. andChaudhary, A., “A Solution Method for Planar and Axisymmetric Contact Problems,”Int. J. Num. Meth. Eng.,21,65–88 (1985).
Joo, J.W. andKwak, B.M., “Analysis and Applicatons of Elastoplastic Contact Problems Considering Large Deformation,”Comp. and Struct.,24,953–961 (1986).
Vanderplaats, G.N., Numerical Optimization Techniques for Engineering Design, McGraw-Hill, New York, 195–203 (1984).
Yamada, Y., Yoshimura, N. andSakurai, T., “Plastic Stress-strain Matrix and its Application for the Solution of Elasto-plastic Problems by the Finite Element Method,”Int. J. Mech. Sci.,10,343–354 (1968).
Hibbit, H.D., Marcal, P.V. andRice, J.R., “A Finite Element Formulations for Problems of Large Strain and Large Displacement,”Int. J. Solids and Struct.,6,1069–1086 (1970).
Determination of Residual Stresses by the Hole-drilling Strain-gage Method, ASTM E837-81.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Joo, J.W., Kwak, B.M. Simulation of three-point bending at large deflections by an elastoplastic contact analysis. Experimental Mechanics 29, 460–465 (1989). https://doi.org/10.1007/BF02323868
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF02323868