Conclusion
The method proposed is suitable for cases when we do not have available a rheometer enabling to obtain sufficiently accurate rheograms for lower values of rates of shear, so long as the parameters of the rheological model chosen are sufficient for expressing the rheogram.
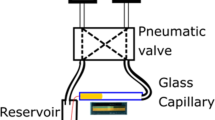
The method has been verified for the power law model by measurements for one liquid (one per cent aqueous solution of carboxymethylcellulose); the measurements were carried out withUbbelohdes modification of the rheometer proposed and also with the rotational rheometer “Rheotest”.
The application of theV-t nomogram is illustrated in fig. 2. Results obtained by using theV-t nomogram and by computation from the relation
[19] are in\(\mathfrak{F}, \mathfrak{B}\) coordinates compared in fig. 3 with those obtained with the “Rheotest” instrument.
Over the range of rates of shear from 20 to 60 sec−1 the agreement in the results was better than 2% relative; this is less than the dispersion of the results of each method.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
Abbreviations
- D sec−1):
-
rate of shear
- g (cm · sec−2):
-
acceleration of gravity
- h (cm):
-
difference in heights in liquid level
- H (cm):
-
maximum value ofh
- L 0 (cm):
-
calibrated length of burette
- L c (cm):
-
length of capillary
- ΔP (dyn · cm−2):
-
pressure drop
- Q (cm3 · sec−1):
-
volumetric flow rate
- R 0 (cm):
-
internal radius of burette
- R c (cm):
-
internal radius of capillary tube
- t (sec):
-
time of flow
- V (cm3):
-
volume of liquid flown out of the instrument
- τ (dyn · cm−2):
-
shear stress
- ϱ (g · cm−3):
-
density of liquid
- \(\mathfrak{F} (sec^{ - 1} )\) :
-
kinematic consistency variable
- \(\mathfrak{B} (dyn \cdot cm^{ - 2} )\) :
-
dynamic consistency variable
- A (1):
-
dimensionless dynamic consistency variable
- B (1):
-
dimensionless kinematic consistency variable
- p (1):
-
dimensionless rate of shear
- T (1):
-
dimensionless time
- y (1):
-
dimensionless pressure drop
- ϑ (1):
-
dimensionless shear stress
References
Wein, O. andJ. Ulbrecht, Rheol. Acta7, 163 (1968).
Coleman, B. D., H. Markowitz andW. Noll, “Viscometric flows of Non-Newtonian Fluids” (Berlin-Heidelberg-New York 1966).
Rabinowitsch, B., Z. Phys. Chem.145 A, 1 (1929).
Pawlowski, J., Rheol. Acta6, 54 (1967).
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Wein, O. V-t capillary rheometry. Rheol Acta 8, 17–22 (1969). https://doi.org/10.1007/BF02321351
Received:
Issue Date:
DOI: https://doi.org/10.1007/BF02321351