Control of the motion of a vessel with a heavy inhomogeneous liquid

Abstract

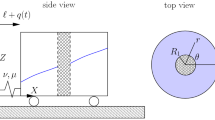
The problem of controlling the internal waves inside a closed rectangular cavity filled with a heavy two-layer fluid is considered in the linear approximation. The fluid is assumed to be stably stratified, ideal, and incompressible. The controlling horizontal force is applied to the body containing the cavity. It is assumed that at the initial moment there are no oscillations of the fluid and the interface is horizontal. The problem is to bring the vessel as a whole into a prescribed state of linear motion without relative wave motion of the fluid. The Cauchy-Poisson problem and the self-consistent integro-differential equation of the vessel motion are solved using the Fourier method and taking into account the reaction of the internal waves. On the basis of an analysis of the corresponding generalized momentum problem, approaches are proposed for solving the problem of control. It is shown that a control action with a sufficiently high order of Steklov smoothness ensures the approximate solution of the control problem with the required accuracy for all the characteristics of the motion of the hybrid oscillating system under consideration.