Abstract
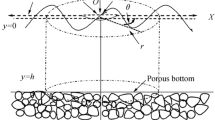
Non-linear and solitary surface waves represent one of the most intriguing and thoroughly investigated phenomena in ocean dynamics. Up to now, a considerable number of results have been obtained, which are related to the study of solitary waves in the coastal shelf zone, and their propagation and transformation under the effect of various factors. In the majority of such studies, the sea bottom surface was assumed to be impervious to fluid. Only some of them, e.g. refs 1–4, considered the propagation of waves in the limited layers of fluids on the pervious (porous) bases. At the same time, Shepard [5] and Nikolaevsky [6] pointed out that the bottom surface structure on the shelf is often porous. In this case, the pervious layer represents a porous matrix (possibly deformable) completely filled with fluid. Its density is different from the free fluid density.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Yamomoto, T., Koning, H. L., Sellmeijer, R. and Hijum, E. V. On the response of a poro-elastic bed to water waves.J. Fluid Mech. (1978)87, 193–206.
Slezkin, N. A. On the influence of a porous bottom on a plane standing wave in a heavy fluid.Izv. Akad. Nauk SSSR, Mekh. Zhidk. Gaza (1987)4, 160–163.
Saks, S. E. Gravity waves in the flux of a heavy fluid with a permeable bottom.Izv. Akad. Nauk SSSR, Mekh. Zhidk. Gaza (1987)2, 115–118.
Stolyarov, I. V. and Taktorov, N. G. Propagation of surface waves in the layer of fluid on a porous base.Izv. Akad. Nauk SSSR, Mekh. Zhidk. Gaza (1987)5, 183–185.
Shepard, F. P.Submarine Geology. New York: Harper & Row (1956).
Nikolaevsky, V. N.Mechanics of Porous and Fractured Media. Moscow: Nedra (1984).
Korsunsky, S. V. Non-linear surface waves in a layer of electric conductive fluid on a porous base.Magn. Hydrodynamics (1991)1, 81–85.
Collins, R.Flows of Fluids through Porous Materials. Moscow: Mir (1964) (in Russian).
Polubarinova-Kochina, P. Ya.The Theory of Movement of Soil Waters. Moscow: Nauka (1977).
Benjamin, T. B. Internal waves of permanent form in fluids of great depth.J. Fluid. Mech. (1967)29, 559–592.
Selezov, I. T. and Korsunsky, S. V.Non-stationary and Non-linear Waves in Electrically Conductive Media. Kiev: Naukova Dumka (1961).
Lamb, G. L.Introduction to Solution Theory. Moscow: Mir (1983) (in Russian).
Korsunsky, S. V. One kind of the perturbed Korteweg-de Vries equation.ZAMM (1992).
Whitham, G. B.Linear and Non-linear Waves. New York: John Wiley (1974).
Yuen, H. C. and Lake, B.Non-linear Dynamics of Gravity Waves in Deep Water. Moscow: Mir (1987).
Ott, E. and Sudan, R. N. Damping of solitary waves.Phys. Fluids (1970)713, 1432–1434.
Additional information
Translated by Mikhail M. Trufanov. UDK 532.59.
Rights and permissions
About this article
Cite this article
Korsunsky, S.V. Non-linear surface waves in the layer of fluid on a porous base. Phys. Oceanogr. 5, 27–34 (1994). https://doi.org/10.1007/BF02197566
Issue Date:
DOI: https://doi.org/10.1007/BF02197566