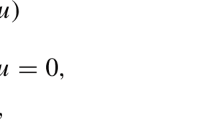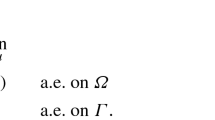Skip to main content
SpringerLink
Log in

Necessary conditions for optimality in the identification of elliptic systems with parameter constraints

  • Contributed Papers
  • Published:
Journal of Optimization Theory and Applications Aims and scope Submit manuscript

Abstract

We consider the problems of dientifying the parametersa ij (x), b i (x), c(x) in a 2nd order, linear, uniformly elliptic equation,

$$\begin{gathered} - \partial _i (a_{ij} (x)\partial _j u) + b_i (x)\partial _i u + c(x)u = f(x),in\Omega , \hfill \\ \partial _v u|_{\partial \Omega } = \phi (s),s \in \partial \Omega , \hfill \\ \end{gathered} $$

on the basis of measurement data

$$u(s) = z(s),s \in B \subset \partial \Omega ,$$

with an equality constraint and inequality constraints on the parameters. The cost functionals are one-sided Gâteaux differentiable with respect to the state variables and the parameters. Using the Duboviskii-Milyutin lemma, we get maximum principles for the identification problems, which are necessary conditions for the existence of optimal parameters.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Anikonov, Yu. E.,Generating Functions, Evolution Equations, and Inverse Problems, Doklady Akademii Nauk, Vol. 323, pp. 172–174, 1992 (In Russian).

    Google Scholar 

  2. Banks, H. T., andKunisch, K.,Estimation Techniques for Distributed-Parameter Systems, Birkhäuser, Boston, Massachusetts, 1989.

    Google Scholar 

  3. Banks, H. T., Reich, S., andRosen, I. G.,An Approximation Theory for the Identification of Nonlinear Distributed-Parameter Systems, SIAM Journal on Control and Optimization, Vol. 28, pp. 523–569, 1990.

    Google Scholar 

  4. Barbu, V.,The Approximate Solvability of the Inverse One-Phase Stefan Problem, International Series of Numerical Mathematics, Vol. 99, pp. 33–43, 1991.

    Google Scholar 

  5. Belov, Yu. Ya.,On an Inverse Problem for a Semilinear Parabolic Equation, Soviet Mathematics Doklady, Vol. 43, pp. 216–220, 1991.

    Google Scholar 

  6. Cannon, J. R., andRundell, W.,An Inverse Problem for an Elliptic Partial Differential Equation, Journal of Mathematical Analysis and Applications, Vol. 126, pp. 329–340, 1987.

    Google Scholar 

  7. Chavent, G.,Identification of Distributed-Parameter Systems: About the Output Least-Square Method, Its Implementation, and Identifiability, Identification and System Parameter Estimation, Edited by R. Isermann, Pergamon, New York, New York, pp. 85–97, 1982.

    Google Scholar 

  8. Chen, Y. M., andZhang, F. G.,Hierarchical Multigrid Strategy for Efficiency Improvement of the GPST Inversion Algorithm, Applied Numerical Mathematics, Vol. 6, pp. 431–446, 1990.

    Google Scholar 

  9. Friedman, A., andGustafsson, B.,Identification of the Conductivity Coefficient in an Elliptic Equation, SIAM Journal on Mathematical Analysis, Vol. 18, pp. 777–787, 1987.

    Google Scholar 

  10. Guyon, F., andYvon, J. P.,On a Weighing Method Improving the Identifiability of Distributed-Parameter Systems, Lecture Notes in Control and Information Sciences, Springer Verlag, Berlin, Germany, Vol. 149, pp. 104–119, 1991.

    Google Scholar 

  11. Hu, S. J., andYu, W. H.,Identification of the Surface Temperature in a Floated Gyroscope, Proceedings of the 3rd IFAC Symposium of Control of Distributed-Parameter Systems, Toulouse, France, pp. 347–352, 1982.

  12. Isakov, V.,Inverse Source Problems, American Mathematical Society, Providence, Rhode Island, 1990.

    Google Scholar 

  13. Korn, R. V., andVogelius, M.,Determining Conductivity by Boundary Measurements, Communications on Pure and Applied Mathematics, Vol. 37, pp. 289–298, 1984.

    Google Scholar 

  14. Lavrent'ev, M. M., Romanov, V. G., andShishatskii, X. X.,Ill-Posed Problems of Mathematical Physics and Analysis, Translations of Mathematical Monographs, American Mathematical Society, Providence, Rhode Island, Vol. 64, 1986.

    Google Scholar 

  15. Romanov, V. G.,Inverse Problems of Mathematical Physics, VNU Science Press BV, Utrecht, Netherlands, 1987.

    Google Scholar 

  16. Suzuki, T.,Gelfand-Levitan Theory and Related Inverse Problems, Inverse Problems: Proceedings of a Conference Held at the Mathematical Research Institute, Oberwolfach, Germany, 1986; Edited by J. R. Cannon and U. Hornung, Birkhäuser Verlag, Basel, Switzerland, pp. 163–171, 1986.

    Google Scholar 

  17. Sylvester, J., andUhlmann, G.,Inverse Boundary-Value Problems at the Boundary-Continuous Dependence, Communications of Pure and Applied Mathematics, Vol. 41, pp. 197–219, 1988.

    Google Scholar 

  18. Yu, W. H.,On Well-Posedness of Inverse Problems for a Class of Hyperbolic Equations, Chinese Mathematical Annals, Vol. 10, pp. 1–9, 1988.

    Google Scholar 

  19. Yu, W. H.,A Rapid Convergent Iteration Method for Identifying Distributed Parameters in Partial Differential Equations, IFAC Symposium on Identification and System Parameter Estimation, Beijing, China, 1988.

  20. Yu, W. H., andSeinfeld, J. H.,Identification of Parabolic Distributed-Parameter Systems by Regularization with Differential Operators, Journal of Mathematical Analysis and Applications, Vol. 132, pp. 365–398, 1988.

    Google Scholar 

  21. Yu, W. H., andSeinfeld, J. H.,Identification of Distributed-Parameter Systems with Pointwise Constraints on the Parameters, Journal of Mathematical Analysis and Applications, Vol. 136, pp. 497–520, 1988.

    Google Scholar 

  22. Gilgarg, D., andTrudinger, N. S.,Elliptic Partial Differential Equations of Second Order, Springer Verlag, New York, New York, 1977.

    Google Scholar 

  23. Girsanov, I. V.,Lectures on the Mathematical Theory of Extremum Problems, Lecture Notes in Economics and Mathematical Systems, Springer Verlag, Berlin, Germany, Vol. 67, 1972.

    Google Scholar 

  24. Zeidler, E.,Nonlinear Functional Analysis and Its Applications, Vol. 3: Variational Methods and Optimization, Springer Verlag, Berlin, Germany, 1985.

    Google Scholar 

  25. Dunford, N., andSchwartz, J. T.,Linear Operators, Vol. 1, Interscience Publishers, New York, New York, 1958.

    Google Scholar 

  26. Lusternik, L. A., andSobolev, V. J.,Elements of Functional Analysis, Hindustan Publishing Corporation, Delhi, India, 1961.

    Google Scholar 

  27. Lions, J. L., andMagenes, E.,Nonhomogeneous Boundary-Value Problems and Applications, Vols. 1–2, Springer Verlag, New York, New York, 1972.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Tianjin University, Tianjin, People's Republic of China

    W. H. Yu (Professor)

Authors
  1. W. H. Yu
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Communicated by L. D. Berkovitz

This research was partially supported by the National Science Foundation of China under Grant No. 19271040.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Yu, W.H. Necessary conditions for optimality in the identification of elliptic systems with parameter constraints. J Optim Theory Appl 88, 725–742 (1996). https://doi.org/10.1007/BF02192207

Download citation

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF02192207

Key Words

Search

Navigation