Abstract
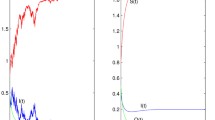
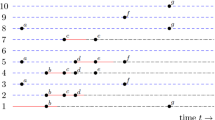
This note begins by reviewing the Kermack-McKendrick and Whittle Threshold Theorems for the general epidemic. It then extends these results to the case of the general epidemic with bunching where theβxy homogeneous mixing term is replaced byβxy/(x+y)α, 0≤α≤1.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
N.T.J. Bailey,The Mathematical Theory of Infectious Diseases (Griffin, London, 1975).
W.O. Kermack and A.G. McKendrick, Contributions to the mathematical theory of epidemics, Proc. Roy. Soc. A115(1927)700.
P. Whittle, The outcome of a stochastic epidemic — a note on Bailey's paper, Biometrika 42(1955)116.
I.W. Saunders, A model for myxomatosis, Math. Biosciences 48(1980)1.
J. Gani and P. Purdue, Matrix-geometric methods for the general stochastic epidemic, IMA J. Appl. Med. Biology 1(1984)333.
Author information
Authors and Affiliations
Additional information
Research supported by Office of Naval Research Contract N00014-84-K-0568.
Rights and permissions
About this article
Cite this article
Gani, J. A note on threshold theorems for epidemics with bunching. Ann Oper Res 8, 207–215 (1987). https://doi.org/10.1007/BF02187092
Issue Date:
DOI: https://doi.org/10.1007/BF02187092