Abstract
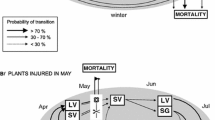
A Leslie-Lewis matrix projection model and a Markov chain model for whole plant growth in the giant Kelp,Macrocystis pyrifera, are developed and compared. Parameters of the models are estimated from field data gathered from several plants in New Zealand over a four-month period. Interpretations of the results are discussed.
Similar content being viewed by others
References
Anderson N (1974) A mathematical model for the growth of giant kelp. Simulation (April): 97–106.
Bosch CA (1971) Redwoods: A population model. Science 172: 345–349.
Clendenning KA (1964) Photosynthesis and growth inMacrocystis pyrifera. Proc. 4th International Seaweed Symposium: 55–65.
Coon D (1981) Studies of whole plant growth inMacrocystis angustifolia. Bot. mar. 24: 19–27.
Enright N, Ogden J. (1979) Applications of transition matrix models in forest dynamics:Araucaria in Papua New Guinea andNothofagus in New Zealand. Australian J. Ecol. 4: 3–23.
Gerard VA, Kirkman H (1984) Ecological observations on a branched, loose-lying form ofMacrocystis pyrifera (L. ) C. Agardh in New Zealand. Bot. mar. 27: 105–109.
Jackson GA (1987) Modeling the growth and harvest yield of the giant kelpMacrocystis pyrifera. Mar. Biol. 95: 611–624.
Kain (Jones) JM (1982) Morphology and growth of the giant kelpMacrocystis pyrifera in New Zealand and California. Mar. Biol. 67: 143–157.
Lefkovitch LP (1965) The study of population growth in organisms grouped by stages. Biometrics 21: 1–18.
Leslie PH (1945) On the use of matrices in certain population mathematics. Biometrica 33: 183–212.
Leslie PH (1948) Some further notes on the use of matrices in population mathematics. Biometrica 35: 213–245.
Lewis EG (1942). On the generation and growth of a population. Sankya 6: 93–96.
Lobban CS (1978a) Translocation of14C inMacrocystis pyrifera (Giant Kelp). Pl. Physiol. 61: 583–589.
Moore LB (1943) Observations on the growth ofMacrocystis in New Zealand. Trans. r. Soc. N. Z. 72: 333–340.
North WJ (1971) Growth of the mature giant kelp. In North W (ed.). The Biology of Giant Kelp Beds (Macrocystis) in California. Nova Hedwigia 32: 123–168.
North WJ (1961) Life-span of the fronds of the giant kelp,Macrocystis pyrifera. Nature 190: 1214–1215.
Pennycuick CJ, Compton RM, Beckingham L (1968). A computer model for simulating the growth of a population, or of two interacting populations. J. theor. Biol. 18: 316–329.
Roberts FS (1976) Discrete mathematical models with applications to Social, Biological, and Environmental Problems. Prentice-Hall, Englewood Cliffs.
Skellam JG (1966). Seasonal periodicity in theoretical population ecology. Proc Fifth Berkeley Symposium on Mathematics, Statistics and Probability 4: 179–205.
Skellam JG (1972). Some philosophical aspects of mathematical modeling in empirical science with special reference to ecology. Symposium Br. ecol. Soc. 2: 13–28.
Strang G (1988) Linear Algebra and its Applications (3rd edn.). Harcourt, Brace, Jovanovich. San Diego.
Usher MB (1966) A matrix approach to the management of renewable resources, with special reference to selection forests. J. appl. Ecol. 3: 355–367.
Usher MB (1969) A matrix model for forest management. Biometrics 25: 309–315.
Usher MB (1972) Developments in the Leslie Matrix Model. In: Jeffers JNR (ed.), Mathematical Models in Ecology: Twelfth Symp. British Ecological Society. Blackwell, Oxford, 29–60.
Usher MB (1976) Extensions to models used in renewable resource management, which incorporate an arbitrary structure. J. environ. Management. 4: 123–140.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Nyman, M.A., Brown, M.T., Neushul, M. et al. Macrocystis pyrifera in New Zealand: testing two mathematical models for whole plant growth. J Appl Phycol 2, 249–257 (1990). https://doi.org/10.1007/BF02179782
Received:
Revised:
Accepted:
Issue Date:
DOI: https://doi.org/10.1007/BF02179782