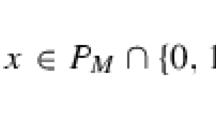Abstract
Quadratic programming, symmetry, positive (semi) definiteness and the linear complementary problem were generalized by Morris and Todd to oriented matroids. Todd gave a constructive solution for the quadratic programming problem of oriented matroids. Using Las Vergnas' lexicographic extension and Bland's basic tableau construction Todd generalized Lemke's quadratic programming algorithm for this problem.
Here some generalizations of Terlaky's finite criss-cross method are presented for oriented matroid quadratic programming. These algorithms are based on the smallest subscript rule and on sign patterns, and do not preserve feasibility on any subsets. In fact two variants of the generalized criss-cross method are presented. Finally two special cases (oriented matroid linear programming and the definite case) are discussed.
Similar content being viewed by others
References
M. L. Balinski andA. W. Tucker, Duality theory of linear programs: A constructive approach with applications,SIAM Review,11 (1969), 347–377.
E. M. L. Beale, On quadratic programming,Naval Research Logistics Quarterly,6 (1959), 227–244.
M. J. Best, Equivalence of some quadratic programming algorithms,Mathematical Programming,30 (1984), 71–87.
R. G. Bland, New finite pivoting rules for the simplex method,Mathematics of Operations Research,2 (1977), 103–107.
R. G. Bland, A combinatorial abstraction of linear programming,J. Combinatorial Theory Ser. B.,23 (1977), 33–57.
R. G. Bland andM. Las Vergnas, Orientability of matroids,J. Combinatorial Theory Ser. B.,24 (1978), 94–123.
Y. Y. Chang andR. W. Cottle, Least index resolution of degeneracy in quadratic programming,Mathematical Programming,18 (1980), 127–137.
R. W. Cottle, The principal pivoting method of quadratic programming, in:Mathematics of the Decision Sciences Part I. Eds. G. B. Dantzig and A. F. Veinott, Lectures in Applied Mathematics, 11 (American Mathematical Society, Providence, R. I., (1968), 142–162.
R. W. Cottle andG. B. Dantzig, Complementary pivot theory of mathematical programming,Linear Algebra and its Applications,1 (1986), 103–125.
G. B. Dantzig,Linear programming and Extensions, Princeton University Press, Princeton, N. J., 1963.
J. Folkman andJ. Lawrence, Oriented matroids,J. Combinatorial Theory Ser. B.,25 (1978), 199–236.
K.Fukuda, Oriented matroid programming,Ph. D. dissertation, University of Waterloo, 1982.
D.Jensen, Coloring and Duality: Combinatorial Augmentation methods,Ph. D. dissertation School of OR and IE, Cornell University, 1985.
E. Keller, The general quadratic optimization problem,Mathematical Programming,5 (1973), 311–337.
E.Klafszky and T.Terlaky, Variants of the „Hungarian Method” for solving linear programming problems,Optimization (accepted for publication).
E.Klafszky and T.Terlaky, Some generalizations of the criss-cross method for quadratic programming,Mathematics of Operations Research (to appear).
M. Las Vergnas, Bases in oriented matroids,J. Combinatorial Theory Ser. B.,25 (1978), 283–289.
M. Las Vergnas, Convexity in oriented matroids,J. Combinatorial Theory Ser. B.,29 (1980), 231–243.
J. Lawrence, Oriented matroids and multiply ordered sets,Linear Algebra and its Applications,48 (1982), 1–12.
C. E. Lemke, Bimatrix equilibrium points and mathematical programming,Management Science,11 (1965), 681–689.
W. D.Morris, Oriented matroids and the linear complementarity problem,Ph. D. thesis. School of OR and IE, Cornell University, 1986.
W. D.Morris and M. J.Todd, Symmetry and positive definiteness in oriented matroids,Cornell University, School of OR and IE, Itacha, Itacha N. Y. Technical Report No.631.
R. T. Rockafellar, The elementary vectors of a subspace ofR n, inCombinatorial Mathematics and its Applications, Proc. of the Chapel Hill Conference, 1967 (R. G. Bore and T. A. Dowling, Eds.) 104–127, Univ. of North Carolina Press, Chapel Hill. 1969.
K.Ritter, A dual quadratic programming algorithm,Univ. of Wisconsin-Madison, Mathematics Research Center, Technical Summary Report, No. 2733 (1984).
C.Roos, On the Terlaky path in the umbrella graph of a linear programming problem,Reports of the Department of Informatics, Delft University of Technology, No. 85-12.
T. Terlaky, A convergent criss-cross method,Optimization,16 (1985), 5, 683–690.
T. Terlaky, A finite criss-cross method for oriented matroids,J. Combinatorial Theory Ser. B.,42 (1987), 319–327.
T. Terlaky, A new algorithm for quadratic programming,European Journal of Operations Research,32 (1987), 294–301.
T. Terlaky, Onlp programming,European Journal of Operations Research,22 (1985), 70–101.
M. J. Todd, Complementarity in oriented matroids,SIAM J. Alg. Disc. Math.,5 (1984), 467–485.
M. J. Todd, Linear and quadratic programming in oriented matroids,J. Combinatorial Theory Ser. B.,39 (1985), 105–133.
A. W. Tucker, Principal pivotal transforms of square matrices,SIAM Review,5 (1963), 305.
C. Van de Panne andA. Whinston, The symmetric formulation of the simplex method for quadratic programming,Econometrica,37 (1969), 507–527.
D. A.Welsh, Matroid theory,Academic Press, 1976.
P. Wolfe, The simplex method for quadratic programming,Econometrica,27 (1959), 382–398.
Zh. Wang, A finite conformal-elimination-free algorithm for oriented matroid programming,Chinecse Annals of Mathematics,8B. No. 1 (1987).
H. Whitney, On the abstract properties of linear dependence,Amer. J. Math.,57 (1935), 507–553.
S. Zionts, The criss-cross method for solving linear programming problems,Management Science,15 (1969), 426–445.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Klafszky, E., Terlaky, T. Some generalizations of the criss-cross method for the linear complementarity problem of oriented matroids. Combinatorica 9, 189–198 (1989). https://doi.org/10.1007/BF02124679
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF02124679