Plane problems of a finite disc containing an internal crack

Abstract

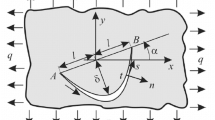
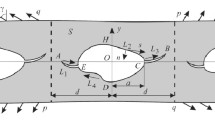
Using complex variable methods in elasticity, this paper deals with the plane problems of a finite disc containing an internal linear crack at any position under general loads. obtains the general forms of complex stress functions and stress-intensity factors. expressed in terms of series, and to these problems discusses three special cases i.e. the cases of the crack under a uniform pressure, a uniform shear stress and the case of the disc rotating uniformly. In these cases the approximate formulas calculating the stress-intensity factors are also presented. The calculated results show that for the middle and small cracks situated inside the disc and not near the external boundary, these approximate formulas give good or better approximation.