Skip to main content
SpringerLink
Log in

An algorithm for the mixed-integer nonlinear bilevel programming problem

  • Published:
Annals of Operations Research Aims and scope Submit manuscript

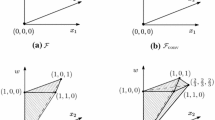
Abstract

The bilevel programming problem (BLPP) is a two-person nonzero sum game in which play is sequential and cooperation is not permitted. In this paper, we examine a class of BLPPs where the leader controls a set of continuous and discrete variables and tries to minimize a convex nonlinear objective function. The follower's objective function is a convex quadratic in a continuous decision space. All constraints are assumed to be linear. A branch and bound algorithm is developed that finds global optima. The main purpose of this paper is to identify efficient branching rules, and to determine the computational burden of the numeric procedures. Extensive test results are reported. We close by showing that it is not readily possible to extend the algorithm to the more general case involving integer follower variables.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. E. Aiyoshi and K. Shimizu, Hierarchical decentralized systems and its new solution by a barrier method, IEEE Trans. Systems, Man, and Cybernetics SMC-11(1981)444–449.

    Google Scholar 

  2. G. Anandalingam and D. White, A penalty function approach for solving bilevel linear programs, Working Paper, Department of Systems, University of Pennsylvania (1988).

  3. J.F. Bard, Coordination of a multidivisional firm through two levels of management, Omega 11(1983)457–468.

    Google Scholar 

  4. J.F. Bard, Convex two-level optimization, Math. Progr. 40(1988)15–27.

    Google Scholar 

  5. J.F. Bard and J.T. Moore, A branch and bound algorithm for the linear bilevel programming problem, SIAM J. Sci. Statist. Comput. 11(1990)281–292.

    Google Scholar 

  6. J.F. Bard and J.E. Falk, An explicit solution to the multi-level programming problem, Comput. Oper. Res. 9(1982)77–100.

    Google Scholar 

  7. T. Basar and H. Selbuz, Closed loop Stackelberg strategies with applications in optimal control of multilevel systems, IEEE Trans. Auto. Control AC-24(1979)166–178.

    Google Scholar 

  8. W.F. Bialas and M.H. Karwan, On two-level optimization, IEEE Trans. Auto. Control AC-27(1982)211–214.

    Google Scholar 

  9. W. Candler and R. Townsley, A linear two-level programming problem, Comput. Oper. Res. 9(1982)59–76.

    Google Scholar 

  10. R. Cassidy, M.J. Kirby and W.M. Raike, Efficient distribution of resources through three levels of government, Manag. Sci. 17(1971)462–473.

    Google Scholar 

  11. T.A. Edmunds, Algorithms for nonlinear bilevel mathematical programs, Ph.D. Dissertation, Department of Mechanical Engineering, University of Texas at Austin (1988).

  12. Y. Fan, S. Sarkar and L. Lasdon, Experiments with successive quadratic programming algorithms, Working Paper, Department of General Business, University of Texas, Austin (1985).

    Google Scholar 

  13. J. Fortuny-Amat and B. McCarl, A representation and economic interpretation of a two-level programming problem, J. Oper. Res. Soc. 32(1981)783–792.

    Google Scholar 

  14. P. Hansen, B. Jaumard and G. Savard, A variable elimination algorithm for bilevel linear programming, RUTCOR Research Report RRR 17–89, Rutgers University (1989).

  15. J. Júdice and A. Faustino, The solution of the linear bilevel programming problem by using the linear complementarity problem, Investigacao Operacional 8(1988)77–95.

    Google Scholar 

  16. P.B. Luh, T.S. Chang and T.K. Ning, Three-level hierarchical decision problems,Proc. 5th MIT/ONR Workshop on Command, Control, and Communications Systems, Monterey, CA (1982).

  17. J.T. Moore and J.F. Bard, The mixed integer bilevel programming problem, Oper. Res. 38(1990)911–921.

    Google Scholar 

  18. M. Simaan and J.B. Cruz, Jr., On the Stackelberg strategy in nonzero-sum games, J. Optim. Theory Appl. 11(1973)533–555.

    Google Scholar 

  19. J. Singhal, R.E. Marsten and T.L. Morin, Fixed order branch-and-bound methods for mixed-integer programming: The ZOOM system, ORSA J. Comput. 1(1989)44–51.

    Google Scholar 

  20. B. Tolwinski, Closed-loop Stackelberg solution to a multi-stage linear-quadratic game, J. Optim. Theory Appl. 34(1981)485–501.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Systems Research Group, Lawrence Livermore National Laboratory, University of California, 94550, Livermore, CA, USA

    Thomas A. Edmunds

  2. Department of Mechanical Engineering, Operations Research Group, University of Texas, 78712, Austin, TX, USA

    Jonathan F. Bard

Authors
  1. Thomas A. Edmunds
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jonathan F. Bard
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

This work was supported by a grant from the Advanced Research Program of the Texas Higher Education Coordinating Board.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Edmunds, T.A., Bard, J.F. An algorithm for the mixed-integer nonlinear bilevel programming problem. Ann Oper Res 34, 149–162 (1992). https://doi.org/10.1007/BF02098177

Download citation

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF02098177

Keywords

Search

Navigation