Skip to main content
SpringerLink
Log in

A global formalism for nonlinear waves in conservation laws

  • Published:
Communications in Mathematical Physics Aims and scope Submit manuscript

Abstract

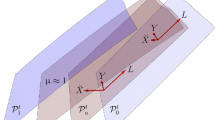
We introduce a unifying framework for treating all of the fundamental waves occurring in general systems ofn conservation laws. Fundamental waves are represented as pairs of states statisfying the Rankine-Hugoniot conditions; after trivial solutions have been eliminated by means of a blow-up procedure, these pairs form an (n+1)-dimensional manifold

, the fundamental wave manifold. There is a distinguishedn-dimensional submanifold of

containing a single one-dimensonal foliation that represents the rarefaction curves for all families. Similarly, there is a foliation of

itself that represent shock curves. We identify othern-dimensional submanifolds of

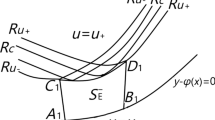
that are naturally interpreted as boundaries of regions of admissible shock waves. These submanifolds also have one-dimensional foliations, which represent curves of composite waves. This geometric framework promises to simplify greatly the study of the stability and bifurcation properties

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Azevedo, A., Marchesin, D.: Multiple Viscous Profile Riemann Solutions in Mixed Elliptic-Hyperbolic Models for Flow in Prorous Media. In: Hyperbolic Equations that Change Type, Keyfitz, B., Shearer, M. (eds). IMA Volumes in Mathematics and its Applications, vol.27, pp. 1–17. Berlin, Heidelberg, New York: Springer 1990

    Google Scholar 

  2. Bethe, H.: The Theory of Shock Waves for an Arbitrary Equation of State. Clearinghouse for Federal Scientific and Technical Information. U.S. Dept. of Commerce, Rep. No. PB-32189, Washington, DC, 1942

  3. Bott, R., Tu, L.: Differential forms in algeraic topology. Berlin, Heidelberg, New York: Springer 1982

    Google Scholar 

  4. Brio, M.: Admissibility conditions for Weak Solutions of Non-Strictly Hyperbolic Systems. In: Nonlinear Hyperbolic Equations-Theory, Computational Methods, and Applications, Ballmann, J., Jeltsch, R. (eds). Notes on Numerical Fluid Mechanics, vol.24, 43–50. Braun-Schweig: Vieweg 1989

    Google Scholar 

  5. Čanić, S.: State Univ. of New York of Stony Brook. Ph.D. Thesis, in preparation, 1992

  6. Čanić, S., Plohr, B.: A global approach to shock wave admissibility. State Univ. of New York at Stony Brook, Report No. SUNYSB-AMS-91-10, 1991

  7. Conley, C., Smoller, J.: Viscosity matrices for two-dimensional nonlinear hyperbolic systems. Commun. Pure Appl. Math.23, 867–884 (1970)

    Google Scholar 

  8. Courant, C., Friedrichs, K.: Supersonic flow and shock waves. New York, NY: John Wiley 1948

    Google Scholar 

  9. Dafermos, C.: Structure of solutions of the Riemann problem for hyperbolic systems of conservation laws. Arch. Radional Mech. Anal.53, 203–217 (1974)

    Google Scholar 

  10. Dafermos, C., DiPerna, R.: The Riemann problem for certain classes of hyperbolic systems of conservation laws. J. Differ. Eqs.20, 90–114 (1976)

    Google Scholar 

  11. Fischer, G.: Complex Analytic Geometry. Lect. Notes in Math., vol.538, Berlin, Heidelberg, New York: Springer 1976

    Google Scholar 

  12. Foy, L.: Steady state solutions of hyperbolic systems of conservation laws with viscous terms. Commun. Pure Appl. Math.17, 177–188 (1964)

    Google Scholar 

  13. Freistühler, H.: Instability of vanishing viscosity approximation to hyperbolic systems of conservation laws with rotational invariance. J. Differ. Eq.87, 205–226 (1990)

    Google Scholar 

  14. Furtado, F.: Structural stability of nonlinear waves for conservation laws. New York Univ., Ph.D. Thesis, 1989

  15. Gelfand, I.: Some problems in the theory of quasi-linear equations. Uspekhi Mat. Nauk14, 87–158 (1959), Am. Math. Soc. Transl. 295–381 (1963)

    Google Scholar 

  16. Glimm, J.: Nonlinear and Stochastic Phenomena: The Grand Challenge for Partial Differential Equations. SIAM Review33, 626–643 (1991)

    Google Scholar 

  17. Golubitsky, M., Guillemin, V.: Stable mappings and their singularities. Berlin, Heidelberg, New York: Springer 1973

    Google Scholar 

  18. Golubitsky, M., Schaeffer, D.: Singularities and groups in bifurcation theory. Berlin, Heidelberg, New York: Springer 1984

    Google Scholar 

  19. Gomes, M. E.: Riemann problems requiring a viscous profile entropy condition, Adv. Appl. Math.10, 285–323 (1989)

    Google Scholar 

  20. Hartshorne, R.: Algebraic geometry, Berlin, Heidelberg, New York: Springer 1977

    Google Scholar 

  21. Holden, H.: On the Riemann problem for a prototype of a mixed type conservation law. Commun. Pure Appl. Math.40, 229–264 (1987)

    Google Scholar 

  22. Isaacson, E.: Global Solution of a Riemann Problem for a Nonstrictly Hyperbolic System of Conservation Laws Arising in Enhanced Oil Recovery. Rockefeller Univ., preprint, 1981

  23. Isaacson, E., Marchesin, D., Plohr, B.: Transitional waves for conservation laws. SIAM J. Math. Anal.21, 837–866 (1990)

    Google Scholar 

  24. Isaacson, E., Marchesin, D., Plohr, B., Temple, J. B.: The Riemann problem near a hyperbolic singularity: The classification of quadratic Riemann problems I. SIAM J. Appl. Math.48, 1009–1032 (1988)

    Google Scholar 

  25. Isaacson, E.: Multiphase flow models with singular Riemann problems. Mat. Appl. Comput. (1992) (to appear)

  26. Isaacson, E., Temple, J. B.: Examples and classification of non-strictly hyperbolic systems of conservation laws. Proceedings of the Am. Math. Soc. Meeting, Anaheim, CA (1985)

  27. —: Analysis of a singular hyperbolic system of conservation laws. J. Diff. Equations65, 250–268 (1986)

    Google Scholar 

  28. —: The Riemann problem near a hyperbolic singularity II. SIAM J. Appl. Math.48, 1287–1301 (1988)

    Google Scholar 

  29. —: The Riemann problem near a hyperboiic singularity III. SIAM J. Appl. Math.48, 1302–1312 (1988)

    Google Scholar 

  30. Kan, P.-T.: On the Cauchy Problem of a 2×2 System of Nonstrictly Hyperbolic Conservation Laws. New York Univ., Ph.D. Thesis, 1989

  31. Keyfitz, B., Kranzer, H.: The Riemann problem for a class of hyperbolic conservation laws exhibiting a parabolic degeneracy. J. Diff. Equations47, 35–65 (1983)

    Google Scholar 

  32. Kobayashi, S., Nomizu, K.: Foundations of differential geometry. Vol I, New York, NY: Interscience 1863

    Google Scholar 

  33. Lax, P.: Hyperbolic systems of conservation laws II. Commun. Pure Appl. Math.10, 537–566 (1957)

    Google Scholar 

  34. —: Hyperbolic systems of conservation laws and the mathematical theory of shock waves. Regional Conference Series Lectures in Applied Mathematics, vol.11, Society for Industrial and Applied Mathematics, Philadelphia, PA, 1973

    Google Scholar 

  35. Leibovich, L.: Solutions of the Riemann problem for hyperbolic systems of quasi-linear equations without convexity conditions. J. Diff. Equations45, 81–90 (1974)

    Google Scholar 

  36. Liu, T.-P.: The Riemann problem for general 2×2 conservation laws. Trans. Am. Math. Soc.199, 89–112 (1974)

    Google Scholar 

  37. —: The Riemann problem for general systems of conservation laws. J. Diff. Equations18, 218–234 (1975)

    Google Scholar 

  38. —: Admissible solutions of hyperbolic conservation laws. Mem. Am. Math. Soc.30, 603–634 (1981)

    Google Scholar 

  39. —: Nonlinear stability of shock waves for viscous conservation laws. Mem. Am. Math. Soc.56, 1–108 (1985)

    Google Scholar 

  40. Liu, T.-P., Xin, X.: Overcompressive Shock Waves, in Nonlinear Evolution Equations that Change Type, Keyfitz, B., Shearer, M. (eds.). IMA Volumes in Mathematics and its Applications, vol.27, pp. 139–145. Berlin, Heidelberg, New York: Springer 1990

    Google Scholar 

  41. Malta, I., Tomei, C.: Singularities of vector fields arising from one-dimensional Riemann problems. J. Diff. Equations94, 165–190 (1991)

    Google Scholar 

  42. Marchesin, D., Palmeira, C. F.: Topology of elementary waves of mixed systems of conservation laws. In preparation, 1992

  43. Medeiros, H.: Stability of hyperbolic singularities for conservation laws in models of flow of three-phase fluids in porous media. Pontificia Universidade Católica do Rio de Janeiro, Ph.D. Thesis (in Portuguese), 1989

  44. Menikoff, R., Plohr, B.: The Riemann problem for fluid flow of real materials. Rev. Mod. Phys.61, 75–130 (1989)

    Google Scholar 

  45. Oleînik, O.: On the uniqueness of the generalized solution of the Cauchy problem for a non-linear system of equations occuring in mechanics. Uspekhi Mat. Nauk12, 169–176 (1957)

    Google Scholar 

  46. Palmeira, C. F.: Line fields defined by eigenspaces of derivatives of maps from the plane to itself. Proceedings of the IVth International Conference of Differential Geometry, Santiago de Compostela, Spain (1988)

  47. Peixoto, M.: Structural stability on two dimensional manifolds. Topology1, 101–120 (1962)

    Google Scholar 

  48. Riemann, B.: Uber die Fortpflanzung ebener Luftwellen von endlicher Schwingungsweite. Göttingen Abhandlungen8, 43 (1958)

    Google Scholar 

  49. Schaeffer, D., Shearer, M.: The classification of 2×2 systems of non-strictly hyperbolic conervation laws, with application to oil recovery. Commun. Pure Appl. Math.40, 141–178 (1987)

    Google Scholar 

  50. Schecter, S.: Simultaneous equilibrium and heteroclinic bifurcation of planar vector fields via the Melnikov integral. Nonlinearity3, 79–99 (1990)

    Google Scholar 

  51. Schecter, S., Shearer, M.: Undercompressive shocks for nonstrictly hyperbolic conservation laws. J. Dyn. Diff. Equations3, 199–271 (1991)

    Google Scholar 

  52. Shearer, M.: Admissibility criteria for shock wave solutions of a system of conservation laws of mixed type. Proc. R. Soc. Edinburgh93A, 233–244 (1983)

    Google Scholar 

  53. —: The Riemann problem for 2×2 systems of hyperbolic conservation laws with case I quadratic nonlinearities. J. Diff. Equations80, 343–363 (1989)

    Google Scholar 

  54. Shearer, M., Schaeffer, D.: Riemann problems for nonstrictly hyperbolic 2×2 systems of conservation laws. Trans. Am. Math. Soc.304, 267–306 (1987)

    Google Scholar 

  55. Shearer, M., Schaeffer, D., Marchesin, D., Paes-Leme, P.: Solution of the Riemann problem for a protoype 2×2 system of non-strictly hyperbolic conservation laws. Arch. Rational Mech. Anal.97, 299–320 (1987)

    Google Scholar 

  56. Shearer, M., Schecter, S.: Riemann problems Involving Undercompressive Shocks. In: PDEs and Continuum Models of Phase Transitions, Rascle, M., Serre, D., Slemrod, M. (eds). Lect. Notes in Phys., vol.344, pp. 187–200. Berlin, Heidelberg, New York: Springer 1989

    Google Scholar 

  57. Slemrod, M.: Admissibility criteria for propagating phase boundaries in a van der Waals fluid. Arch. Rational Mech. Anal.81, 303–319 (1983)

    Google Scholar 

  58. Smoller, J., Johnson, J.: Global solutions for an extended class of hyperbolic systems of conservation laws. Arch. Rational Mech. Anal.32, 169–189 (1969)

    Google Scholar 

  59. Stomayor, J.: Generic one-parameter families of vector fields on two-dimensional manifolds. Publ. Math. IHES43, 5–46 (1974)

    Google Scholar 

  60. Wendroff, B.: The Riemann Problem for Materials with Non-Convex Equations of State: I Isentropic Flow: II General Flow, J. Math. Anal. and Appl.38, 454–466; 640–648 (1972)

    Google Scholar 

  61. Whitham, G.: Linear and nonlinear waves, New York, NY: John Wiley 1974

    Google Scholar 

  62. Wu, C.: On MHD intermediate Shocks. Geophys. Res. Lett.14 (668–671)

  63. Xu, Q.-P.: State Univ. of New York at Stony Brook, Ph.D. Thesis, in preparation, 1992

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, University of Wyoming, P.O. Box 3036 Univ. Station, 82071, Laramie, WY, USA

    Eli L. Issacson

  2. Instituto de Matemática Pura e Aplicada and Department of Mathematics, Pontifícia Universidade Católica, 22460, Rio de Janeiro, RJ, Brazil

    Dan Marchesin

  3. Department of Mathematics, Pontifícia Universidade Católica, 22453, Rio de Janeiro, RJ, Brazil

    C. Frederico Palmeira

  4. Department of Mathematics and of Applied Mathematics and Statistics, State University of New York, 11794-3651, Stony Brook, NY, USA

    Bradley J. Plohr

Authors
  1. Eli L. Issacson
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Dan Marchesin
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. C. Frederico Palmeira
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Bradley J. Plohr
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Communicated by A. Jaffe

This work was supported in part by: the NSF/CNPq U.S.-Latin America Cooperative Science Program under Grant INT-8612605; the Institute for Mathematics and its Applications with funds provided by the National Science Foundation; the Air Force Office of Scientific Research under Grant AFOSR 90-0075; the National Science Foundation under Grant 8901884; the U.S. Department of Energy under Grant DE-FG02-90ER25084; the U.S. Army Research Office under Grant DAAL03-89-K-0017; the Financiadora de Estudos e Projetos; the Conselho Nacional de Desenvolvimento Científico e Tecnológica (CNPq); the Fundação de Amparo à Pesquisa do Estado do Rio de Janeiro (FAPERJ); the Coordenação de Aperfeiçamento de Pessoal de Ensino Superior (CAPES); and the Sociedade Brasileira de Matemática (SBM)

Rights and permissions

Reprints and permissions

About this article

Cite this article

Issacson, E.L., Marchesin, D., Frederico Palmeira, C. et al. A global formalism for nonlinear waves in conservation laws. Commun.Math. Phys. 146, 505–552 (1992). https://doi.org/10.1007/BF02097015

Download citation

  • Received:

  • Revised:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF02097015

Keywords

Search

Navigation