Abstract
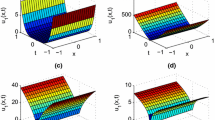
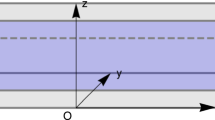
A stable iterative method for solving the nonlinear boundary value problem at nonlinear homogeneous film geometries is presented. The principle of consistency between field power and wavenumber is utilized and the resulting bistable and filtering behavior is investigated.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
W. Chen and D.L. Mills, Physical Review B, Vol. 35, No. 2, pp. 524–532, 15 January 1987.
K.M. Leung, J. Opt. Soc. Am. B, Vol. 5, No. 2, pp. 571–574, February 1988.
K.M. Leung, Physical Review B, Vol. 39, No. 6, pp. 3590–3598, 15 February 1989.
K.M. Leung and R.L. Lin, Physical Review B, Vol. 44, No. 10, pp. 5007–5012, 1 September 1991.
R. Reinisch and G. Vitrant, Physical Review B, Vol. 39, No. 9, pp. 5775–5777, 15 March 1989.
K.L. Stokes and A. Puri, Opt. Let. Vol. 15, No. 17, pp.986–988, 1 September 1990.
C.N. Capsalis, G.S. Barbastathis and C.P. Chronopoulos, Int. J. Infrared and Millim. Waves, Vol. 12, No. 9, September 1991.
G.S.Barbastathis, C.N.Capsalis and C.P.Chronopoulos, 2nd Workshop on Wave Propagation Problems, Foundation for Technology and Research, Iraklion Crete, June 15–16, 1992 (Proceedings under preparation).
S. Dutta Gupta and G.S. Agarwal, J.Opt.Soc.Am. B, Vol.4, No.5, pp. 691–695, 1987.
G.S. Agarwal and S. Dutta Gupta, Optics Letters, Vol. 12, No. 10, pp.829–831, 1987.
S. Dutta Gupta, J.Opt.Soc.Am. B, Vol.6, No. 8, pp.1607–1610, 1989.
G.P. Agrawal, "Nonlinear Fiber Optics", Academic Press, New York 1989.
A. Hasegawa, "Optical Solitons in Fibers", Springer-Verlag, New York 1990.
R.H. Stolen and C. Lin, Phys. Rev. A17, 1448(1978).
A.E. Kaplan, Sov. Phys. JETP, Vol. 45 (5), pp. 896–905, 1977.
A.E. Kaplan, in "Optical Bistability", ed. C.M. Bowden, M. Ciftan and H.R. Robl, Plenum Press, New York 1981.
G.A. Swartzlander and A.E. Kaplan, J. Opt. Soc. Am. B, Vol. 5, No.4, pp. 709–713, April 1988.
R. Frey and B. Thedrez, J.Opt.Soc.Am. B, Vol.5, No. 5, pp. 1176–1180, 1988.
A. Aceves, J.V. Moloney and A.C. Newell, J.Opt.Soc.Am. B, Vol.5, No.2, pp.559–564, 1988.
F. Ouellette and M. Piche, J.Opt.Soc.Am. B, Vol.5, No. 6, 1988.
M.Born and E.Wolf, "Principles of Optics" (6th ed.), Pergamon Press, 1989.
We intend to show similar results in future work that is currently in progress.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Barbastathis, G.S., Capsalis, C.N. Calculations of homogeneous nonlinear film transmittivity using a self-consistent linearizing method. Int J Infrared Milli Waves 15, 1125–1138 (1994). https://doi.org/10.1007/BF02096138
Received:
Issue Date:
DOI: https://doi.org/10.1007/BF02096138