Skip to main content
SpringerLink
Log in

Thermal convection in a nonequilibrium turbulent medium with rotation

  • Published:
Fluid Dynamics Aims and scope Submit manuscript

Abstract

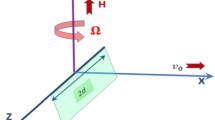
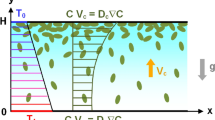
The equations of thermal convection in a rotating plane horizontal layer of nonequilibrium turbulent fluid are obtained, the system of equations is linearized and the boundary value problem is formulated. Some general properties of the perturbation spectrum are found and a solution, which includes the classical solution in the absence of turbulence as a limiting case, is obtained.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. A. S. Monin and A. M. Yaglom,Statistical Fluid Mechanics, Vol. 2, MIT Press, Cambridge, Mass. (1975).

    Google Scholar 

  2. S. S. Moiseev, P. B. Rutkevich, A. V. Tur, and V. V. Yanovskii, “Vortex dynamo in a convective medium with spiral turbulence,”Zh. Eksp. Teor. Fiz.,94, 144 (1988).

    Google Scholar 

  3. Yu. A. Berezin and V. P. Zhukov, “Convective instability in a medium with spiral turbulence,”Zh. Prikl. Mekh. Tekh. Fiz., No. 1, 62 (1990).

  4. Yu. A. Berezin and V. P. Zhukov, “Effect of rotation on the formation of large-scale structures in a turbulent medium,” Preprint No. 17 [in Russian], IPTM SO AN SSSR, Novosibirsk (1988).

  5. V. M. Trofimov, “Hydrodynamics of turbulence including the large-scale part,” Preprint No. 13 [in Russian], ITPM SO AN, SSSR, Novosibirsk (1991).

  6. V. M. Trofimov, “Contribution to the phenomenological vortex model of turbulence,” in:Modeling in Mechanics, Vol. 6, [in Russian], Novosibirsk (1992), p. 137.

  7. G. Nicolis and I. Prigogine,Self-Organization in Non-Equilibrium Systems, Wiley, New York (1977).

    Google Scholar 

  8. L. I. Sedov,A Course of Continuum Mechanics, Wolters-Noordhoff, Grongingen (1971).

    Google Scholar 

  9. S. S. Moiseev, R. Z. Sagdeev, A. V. Tur, et al., “Theory of the formation of large-scale structures in hydrodynamic turbulence,”Zh. Eksp. Teor. Fiz.,85, 1979 (1983).

    Google Scholar 

  10. L. G. Loitsyanskii,Mechanics of Liquids and Gases, Pergamon Press, Oxford (1966).

    Google Scholar 

  11. G. Z. Gershuni and E. M. Zhukhovitskii,Convective Stability of an Incompressible Fluid [in Russian], Nauka, Moscow (1972).

    Google Scholar 

Download references

Authors
  1. Yu. A. Berezin
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. V. M. Trofimov
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Novosibirsk. Translated from Izvestiya Rossiiskoi Akademii Nauk, Mekhanika Zhidkosti i Gaza, No. 6, pp. 62–70, November–December, 1994.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Berezin, Y.A., Trofimov, V.M. Thermal convection in a nonequilibrium turbulent medium with rotation. Fluid Dyn 29, 789–796 (1994). https://doi.org/10.1007/BF02040786

Download citation

  • Received:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF02040786

Keywords

Search

Navigation