Skip to main content
SpringerLink
Log in

Boundary and interior layer behavior for singularly perturbed vector problem

  • Published:
Applied Mathematics and Mechanics Aims and scope Submit manuscript

    We’re sorry, something doesn't seem to be working properly.

    Please try refreshing the page. If that doesn't work, please contact support so we can address the problem.

Abstract

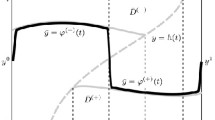
In this paper, we consider the vector nonlinear boundary value problem: εy″=f (x, y, z, y′, ε). y (0)=A1, y (1)=B1 εz″=g(x, y, z, z′, ε), z (0)=A2, z (1)=B2 where ε>0 is a small parameter, 0⩽x⩽1, f and g are continuous functions in R4. Under appropriate assumptions, by means of the differential inequalities, we demonstrate the existence and estimation, involving boundary and interior layers, of the solutions to the above problem.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Mo Jiaqi, The estimation of singularly perturbed solution for a second-order quasilinear equation via differential inequalites,J. Math. Res. Exposition, 1 (1986), 58–64.

    Google Scholar 

  2. Howes, F.A., Effective characterization of the asymptotic behavior of solutions of singularly perturbed boundary value problem,SIAM. J. Appl. Math.,30, 2 (1976), 296–305.

    Google Scholar 

  3. Howes, F.A., Differential inequalities of higher order and the asymptotic solution of nonlinear boundary value problems,SIAM. J. Math. Anal.,13, 1 (1982), 61–82.

    Google Scholar 

  4. Lin Zhong-chi, Some estimations of solution of nonlinear boundary value problem for second order systems,Acta. Mathematica Scientia,7, 2 (1987), 229–239.

    Google Scholar 

  5. Lin Zhong-chi, The higher order approximation of solution of quasilinear second order systems for singular perturbation,Chin. Ann. of Math.,8B, 3 (1987), 357–363.

    Google Scholar 

  6. Chang, G.W., Diagonalization method for a vector boundary value problem of singular perturbation type,J. Math. Anal. Appl.,48 (1974), 652–665.

    Google Scholar 

  7. Kelley, W.G., Existence and uniqueness of solutions for vector problems containing small parameters,J. Math. Anal. Appl.,131 (1988), 295–312.

    Google Scholar 

  8. Lan, Chin-chin, Boundary value problem for second and third order differential equations,J. Diff. Equs.,18, 2 (1975), 258–274.

    Google Scholar 

  9. Liu Guang-xu, On singularly perturbed quasilinear systems,Applied Math. and Mech.,8, 11 (1987), 1027–1036.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Anhui Normal University, Wuhu

    Zhang Xiang

Authors
  1. Zhang Xiang
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Communicated by Lin Zong-chi

The Project Supported by the National Natural Science Foundations of China.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Xiang, Z. Boundary and interior layer behavior for singularly perturbed vector problem. Appl Math Mech 11, 1067–1074 (1990). https://doi.org/10.1007/BF02015690

Download citation

  • Received:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF02015690

Key words

Search

Navigation