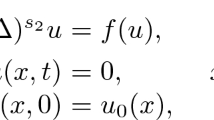Skip to main content
SpringerLink
Log in

Existence, uniqueness and properties of the solutions of a degenerate parabolic equation with diffusion-advection-absorption

  • Published:
Acta Mathematicae Applicatae Sinica Aims and scope Submit manuscript

Abstract

This paper deals with the problems on the equation

$$u_t = A(u)_{xx} + B(u)_x - C(u), (x,t) \in Q_T \subset R \times (0,\infty )$$

in the following three aspects: i) The existence of a continuous weak solution for the Cauchy problem, Cauchy-Dirichlet problem and the first boundary and initial values problem, ii) the uniqueness of the the solutions of the above mentioned three problems, iii) the properties of the solutions. The study on this equation, which has many backgrounds such as the filtrations in porous media as water in soil, is itself important in mathematics as well as in practice.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. M. Bertsch, R. Kersner and L.A. Peletier. Positivity Versus Localization in Degenerate Equations.Nonlinear Analysis, TMP, 1985, 9 (9): 987–1008.

    Google Scholar 

  2. J.I. Diaz, R. Kersner. On a Nonlinear Degenerate Parabolic Equation in Filtration or Evaporation Through a Porous Medium.J. Differential Equations, 1987, 69: 368–403.

    Article  Google Scholar 

  3. L.C. Evans, B.F. Kner. Instantaneous Shrinking of the Support of Nonnegative Solution to Certain Nonlinear Parabolic Equations and Variational Inequalities.Illois J. Math., 1979, 23: 153–166.

    Google Scholar 

  4. A. Friedman. Partial Differential Equations of Parabolic Type. Prentice-Hall, Engle-Wood Cliffs, N.J., 1964.

    Google Scholar 

  5. B.H. Gilding. A Nonlinear Degenerate Parabolic Equation.Ann. Sup. Pisa. (Series IV), 1977, IV (3): 393–432.

    Google Scholar 

  6. B.H. Gilding. Improved Theory for a Nonlinear Degenerate Parabolic Equation.Ann. Scuola Norm, Sup. Pisa CI Sci. (Series IV), 1989, Vol. XVI, Fasc. 2: 165–224.

    Google Scholar 

  7. B.H. Gilding. The Occurrence of Interfaces in Nonlinear Degenerate Parabolic Diffusion-advection Processes.Arch. Rat. Mach. Ana., 1988, 100 (3): 243–263.

    Google Scholar 

  8. R. Kersner. Filtration with Absorption: Necessary and Sufficient Condition for the Propagation of Perturbations to Have Finite Velocity.J. Math. Anal. Appl., 1982, 90: 463–479.

    Article  Google Scholar 

  9. R. Kersner. Degenerate Parabolic Equation with General Nonlinearities.Nonl. Anal. TMP, 1980, 4 (2): 340–347.

    Google Scholar 

  10. R. Kersner. Localization Conditions for Thermal Perturbations in a Semibounded Moving Medium with Absorption.Vest. Mosk. Univ. Mate., 1976, 31 (4): 52–58.

    Google Scholar 

  11. O.A. Ladyzenskaja, V.A. Solonnikov and N.N. Ural'ceva. Linear and Quasi-linear Equations of Parabolic Type. Translations of Mathematical Monographs, Vol.23, American Mathematical Society, Providence, Rhode Island, 1968.

    Google Scholar 

  12. O.A. Oleinik, A.S. Kalashnikov and Chzhou Yui-lin. The Cauchy Problems and Boundary Problems for Equation of Type of Unsteady Filtration.Izv. Akad. Nauk. SSSR ser. Mate., 1958, 22: 667–704.

    Google Scholar 

  13. Chen Chang-sheng. The Propagations of Nonstationary Filtration with Absorption. The Filtration Problem, Vol.2, Dept. of Appl. Math. Tsinghua University, Beijing, 1986, 107–121.

    Google Scholar 

  14. Chen Yazhe. Existence and Uniqueness of Weak Solutions of Uniformly Degenerate Quasi-linear Parabolic Equations.Chin. Ann. of Math., 1985, 6B (2): 131–145.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Applied Mathematics, Tsinghua University, 100084, Beijing, China

    Song Binheng

Authors
  1. Song Binheng
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

This work is supported in part by the Chinese Science Foundation.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Song, B. Existence, uniqueness and properties of the solutions of a degenerate parabolic equation with diffusion-advection-absorption. Acta Mathematicae Applicatae Sinica 10, 113–140 (1994). https://doi.org/10.1007/BF02006112

Download citation

  • Received:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF02006112

Key words

Search

Navigation