Skip to main content
SpringerLink
Log in

Spectral-finite element method for solving two-dimensional vorticity equations

  • Published:
Acta Mathematicae Applicatae Sinica Aims and scope Submit manuscript

Abstract

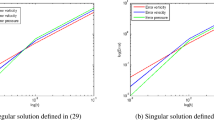
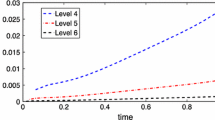
In this paper, we construct a spectral-finite element scheme for solving semi-periodical two-dimensional vorticity equations. The error between the genuine solution and approximate solution is estimated strictly. The numerical results show the advantages of such a method. The technique used in this paper can be easily generalized to three-dimensional problems.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Roache, P.J., Computational Fluid Dynamics, 2nd edition, Hermosa Publishers, 1976.

  2. Raviart, P.A., Approximation numèrique des phenomenes de diffusion convection, Méthods d'éléments finis en méchanque des fluids, Cours a l'École d'été d'analyse numérique, 1979.

  3. Guo Ben-yu, A Class of Difference Schemes for Two-dimensional Viscous Vorticity Equations,Acta Mathematica Sinica,17(1974), 242–258.

    Google Scholar 

  4. Guo Ben-yu, Error Estimation of Spectral Method for Solving Two-dimensional Vorticity Equations,J. Comp. Math.,1(1983), 353–362.

    Google Scholar 

  5. Guo Ben-yu, Spectral-difference Method for Solving Two-dimensional Vorticity Equations,J. Comp. Math.,6(1988), 238–257.

    Google Scholar 

  6. Canuto, C., Maday, Y., Quarteroni, A., Analysis of the Combined Finite Element and Fourier Interpolation,Numer. Math.,39(1982), 205–220.

    Article  Google Scholar 

  7. Canuto, C., Maday, Y., Quarteroni, A., Combined Finite Element and Spectral Approximation of the Navier-Stokes Equations, Numer. Math.,44(1984), 201–217.

    Article  Google Scholar 

  8. Mercier, B., Raugel, G., Résolution d'un probléme aux limites dans un ouvert axisymétrique par éléments finis enr, z et séries de Fourier enθ, RAIRO Numer. Anal.,16(1982), 405–461.

    Google Scholar 

  9. Ciarlet, P.G., The Finite-Element Method for Elliptic Problems, North-Holland, 1978.

  10. Grisvard, P., Equations Differentielles Abstraites,Ann. Sci. Ecole Norm. Sup.,4 (1969), 311–395.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Shanghai University of Science and Technology, Shanghai

    Guo Benyu & Cao Weiming

Authors
  1. Guo Benyu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Cao Weiming
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Guo, B., Cao, W. Spectral-finite element method for solving two-dimensional vorticity equations. Acta Mathematicae Applicatae Sinica 7, 257–271 (1991). https://doi.org/10.1007/BF02005974

Download citation

  • Received:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF02005974

Keywords

Search

Navigation