Pressure drop in alternating curved tubes

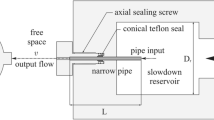
Abstract

Pressure drop measurements in the laminar and turbulent regions for water flowing through an alternating curved circular tube (x=h sin 2πz/λ) are presented. Using the minimum radius of curvature of this curved tube in place of that of the toroidally curved one in calculating the Dean number (ND=Re(D/2R _c )², it is found that the resulting Dean number can help in characterizing this flow. Also, the ratio between the height and length of the tube waves which represents the degree of waveness affects significantly the pressure drop and the transition Dean number. The following correlations have been found:

• 1. For laminar flow:

  $$F_w \left( {\frac{{2R_c }}{D}} \right)^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}} = F_s \left( {\frac{{2R_c }}{D}} \right)^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}} + 0.03,\operatorname{Re}< 2000.$$

• 2. For turbulent flow:

  $$F_w \left( {\frac{{2R_c }}{D}} \right)^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}} = F_s \left( {\frac{{2R_c }}{D}} \right)^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}} + 0.005,2000< \operatorname{Re}< 15000.$$

• 3. The transition Dean number:

  $$ND_{crit} = 5.012 \times 10^3 \left( {\frac{D}{{2R}}} \right)^{2.1} ,0.0111< {D \mathord{\left/ {\vphantom {D {2R_c }}} \right. \kern-\nulldelimiterspace} {2R_c }}< 0.71.$$