Skip to main content
SpringerLink
Log in

Designing parametric blends: surface model and geometric correspondence

  • Published:
The Visual Computer Aims and scope Submit manuscript

Abstract

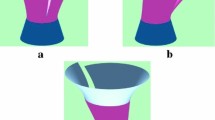
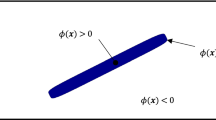
A model based on the curve-modulation technique is proposed for designing a parametric blend between two parametrically defined surfaces. The modulants are the cross section and the spine curves. The end position and tangency conditions of the cross section are discussed. Its intermediate shape can be left to the designer's choice, and generally depends on the application at hand. Various alternative choices, that fulfill the end conditions are suggested; this provides the flexibility demanded by various applications. The spine is designed as the intersection of two derived surfaces. Two alternative surface derivations are proposed, and both are discussed in some detail with their merits and demerits. The first derivation generates the contact curves automatically and relieves the designer from specifying them; the second one accepts contact curves specified by the designer, and generates the spine accordingly. Both of them are equally important in CAD/CAM and solid modelling applications.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Agin GJ, Binford TO (1976) Computer description of curved objects. IEEE Trans Comp, C-25:439

    Google Scholar 

  • Binford TO (1982) Survey of model-based image analysis systems. Int Robotics Res 1(1):18

    Google Scholar 

  • Bloor MIG, Wilson MJ (1989) Generating blend surfaces using partial differential equations. Computer Aided Design 21 (3):165

    Article  Google Scholar 

  • Braid IC (1980) Superficial blends in geometric modelling. CAD Group Document No. 105, University of Cambridge Computer Laboratory

  • Catmull EE, Clark J (1978) Recursively generatedB-spine surfaces on arbitrary topological meshes. Computer Aided Design 10:350

    Article  Google Scholar 

  • Chiyokura H (1987) An extended rounded operation for modelling solids with free form surfaces. (SIGGRAPH '87 Conf Proc) Computer Graphics 21:249

    Google Scholar 

  • Chiyokura H, Kimura F (1983) design of solids with freeform surfaces. (SIGGRAPH '89 Conf Proc) Computer Graphics 17:25

    Google Scholar 

  • Choi BK, Ju SY (1989) Constant radius blending in surface modelling. Computer Aided Design 21:213

    Article  Google Scholar 

  • Choi BK, Lee CS (1990) Sweep surface modelling via coordinate transformations and blending. Computer Aided Design 22:87

    Article  Google Scholar 

  • Coons SA (1967) Surfaces for computer aided design of space forms. MIT Project MAC, MAC-TR 41

  • DePont J (1984) Essays on the cyclide patch. PhD Thesis, University of Cambridge Engineering Department

  • Doo DWH, Sabin MA (1978) Behaviour of recursive division surfaces near extraordinary points. Computer Aided Design 10:356

    Article  Google Scholar 

  • Engeli M (1981) Geometric modelling of complex forms with EUKLID. CIRP '81 Conf Proc Manufacturing Systems 10(2)

  • Farouki RT (1986) The approximation of non-degenerate offset surfaces. Computer Aided Geometric Design 3:15

    Article  Google Scholar 

  • Faux ID, Pratt MJ (1979) Computational geometry for design and manufacture. Ellis Horwood, Chichester

    Google Scholar 

  • Filip D (1989) Blending parametric patches. Tran on Graphics 8(3):164

    Article  Google Scholar 

  • Fajllstrom PO (1986) Smoothing of polyhedral models. (ACM Symposium Conf Proc Computational Geometry 2:226

    Google Scholar 

  • Forrest AR (1977) On Coons' and other methods for the representation of curved surfaces, Computer Graphics Image Proc 1:341

    Article  Google Scholar 

  • Forrest AR (1980) The twisted cubic curve: a computer aided design approach. Computer Aided Design 12:165

    Article  Google Scholar 

  • Hoffman C, Hopcroft J (1985) The potential method for blending surfaces and cornes. Thesis TR 85-699, Cornell University

  • Hoffman C, Hopcroft J (1986) The geometry of projective blending surfaces. Thesis TR 86-758, Cornell University

  • Koparkar PA (1984) Computational techniques for processing parametric curves and surfaces. PhD Thesis, University of Bombay

  • Koparkar P (submitted) Combining subdivision with iterative refinement for detecting intersection of parametric patches

  • Koparkar PA, Mudur SP (1984) Computational techniques for processing parametric surfaces. Computer Vision, Graphics, and Image Proc 28(3):303

    Google Scholar 

  • Koparkar PA, Mudur SP (1985) Subdivision techniques for processing geometric objects. In: Nato ASI Series V F 17: Fundamental Algorithms for Computer Graphics. Springer Berlin Heidelberg New York, p 751

    Google Scholar 

  • Koparkar PA, Mudur SP (1986) Generation of continuous smooth curves resulting from operations on parametric surface patches. Computer Aided Design, 193

  • Middleditch AE, Sears KH (1985) Blend surfaces for set theoretic volume modelling systems. (SIGGRAPH, 85 Conf Proc) Computer Graphics 19(3):161

    Google Scholar 

  • Mudur SP, Koparkar PA (1983) Product surfaces and modulated surfaces for 3-D shape representation in computer vision systems. (IEEE Conf Proc) Man, Cybernetics and Society, p 207

  • Mudur SP, Koparkar PA (1984) Interval methods for processing geometric objects. IEEE Computer Graphics and Applications 4(2):7

    Google Scholar 

  • Nasri AH (1984) Polyhedral division methods for free-form surfaces. PhD Thesis, University of East Anglia

  • Nevatia R, Binford TO (1977) Description and recognition of curved objects. Artificial Intelligence 8:77

    Article  Google Scholar 

  • Rockwood AP, Owen JC (1987) Blend surfaces in solid geometric modelling. Shape Data, Cambridge.

    Google Scholar 

  • Rossignac JR, Requicha AAG (1984) Constant radius blending in solid modelling. Computers in Mechanical Engineering, p 65

  • Sanglikar MA, Koparkar P, Joshi VN (1990) Modelling rolling ball blends for computer aided geometric design. Computer Aided Geometric Design 7(1):1

    Article  Google Scholar 

  • Sanglikar MA, Koparkar P, Joshi VN (submitted): Modelling blends between parametric patches with user specified cross sections, submitted for publication

  • Sanglikar MA, Koparkar P, Joshi VN (1989) Parametric blends for shape modelling. (IEEE TENCON '89 Conf Proc) Information Technologies for 1990

  • Sturge DP, Nicholls MS (1982) Developments in DUCT system of computer aided engineering. (23rd MTDR Conf Proc), p 157

  • Varady T, Vida J, Martin RR (1989) Parametric blending in a boundary representation solid modeller. In: Mathematics of Surfaces 3, Oxford, University Press

  • Willmore TJ (1949) Differential Geometry. Oxford Press

  • Woodwark JR (1987) Blends in geometric modelling. In: The mathematics of surfaces II. Oxford University Press, p 255

  • Zhang D, Bowyer A (1986) CSG set theoretic solid modelling and NC machining of blend surfaces. (Conf Proc ACM Symposium) Computational Geometry

Download references

Author information

Authors and Affiliations

  1. National Center for Software Technology, Gulmohar Cross Road No. 9, Juhu, 400049, Bombay, India

    Pramod Koparkar

Authors
  1. Pramod Koparkar
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Koparkar, P. Designing parametric blends: surface model and geometric correspondence. The Visual Computer 7, 39–58 (1991). https://doi.org/10.1007/BF01994116

Download citation

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF01994116

Key words

Search

Navigation