Abstract
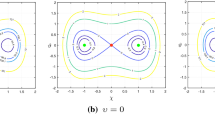
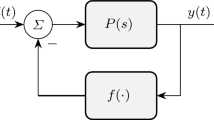
In this paper we analyze some dynamical properties of a chaotic Lorenz system driven by a control input. These properties are the input-state and the input-output feedback linearizability, the stability of the zero dynamics, and the phase minimality of the system. We show that the controlled Lorenz system is feedback equivalent to a controllable linear system. We also show that the zero dynamics are asymptotically stable when the output is an arbitrary state. These facts allow designing control laws such that the closed-loop system has asymptotically stable equilibrium points with dynamic behavior free from chaotic transients. The controllers are robust in the sense that the closed-loop system is stable and non chaotic around a nominal set of parameter values. The results also show that the proposed controllers give better responses compared to linear algorithms obtained from standard linearization techniques, and exhibit a good performance even when the control input is bounded.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Carroll, T. L., and Pecora, L. M., “Synchronizing chaotic circuits,”IEEE Trans. on Circuits and Systems, vol. 38, pp. 453–456, 1991.
Fleming, W. H., et al., “Report of the panel on future directions in control theory: a mathematical perspective”, Society for Industrial and Applied Mathematics, Philadelphia, USA, 1988.
Hartley, T. T. and Mossayebi, F., “Classical control of a chaotic system”, 1st. IEEE Conference on Control Applications, Dayton, Ohio, USA, pp. 522–526, 1992.
Hunt, L. R., Su, R., and Meyer, G., “Global transformations of nonlinear systems”,IEEE Transactions on Automatic Control, vol. 28, pp. 24–31, 1983.
Inaba, N. and Mori, S., “Chaos via torus breakdown in a piece wise-linear forced van der Pol oscillator with a diode,”IEEE Trans. on Circuits and Systems, vol. 38, pp. 398–409, 1991.
Isidori, A.,Nonlinear control systems: an introduction. Springer Verlag, 1989.
Kirchgraber, U. and Stoffer, D., “Chaotic behavior in simple dynamical systems,”SIAM Review, vol. 32, pp. 424–452, 1990.
Lorenz, E. N., “Deterministic non-periodic flow,”J. Atmos. Science, vol. 20, pp. 130–141, 1963.
Khalil, H. K.,Nonlinear systems. MacMillan Publishing Company, 1992.
Mahfouz, I. A. and Badrakhan, F., “Chaotic behavior of some piece wise-linear systems, part II: systems with clearance,”Journal of Sound and Vibration, vol. 143, pp. 289–328, 1990.
Moon, F. C.,Chaotic and fractal dynamics. John Wiley & Sons, Inc., 1992.
Ott, E., Grebogi, C., and Yorke, J. A., “Controlling chaotic dynamical systems,” inChaos/Xaoc: Soviet-American perspectives on nonlinear science, edited by D. K. Campbell. American Institute of Physics, pp. 153–172, 1990.
Spano, M. L. and Ditto, W. L., “Taming chaos experimentally: a primer,”Proc. of the 1st. Experimental Chaos Conference, Arlington, VA, October 1991.
Sparrow, C.,The Lorenz equations: bifurcations, chaos, and strange attractors. Springer Verlag, 1982.
Su, R., Hunt, L., and Meyer, G., “Theory of design using nonlinear transformations,”Proc. of the American Control Conference, USA, pp. 247–251, 1982.
Vincent, T. L. and Yu, J., “Control of a chaotic system,”Dynamics and Control, vol. 1, pp. 35–52, 1991.
Wu, X. and Schelly, Z. A., “Chaotic behavior of chemical systems,”React. Kinet. Catal. Letters, vol. 42, pp. 303–307, 1990.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Alvarez-Gallegos, J. Nonlinear regulation of a Lorenz system by feedback linearization techniques. Dynamics and Control 4, 277–298 (1994). https://doi.org/10.1007/BF01985075
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF01985075