Skip to main content
SpringerLink
Log in

Minimum fuel lunar trajectories for a low-thrust power-limited spacecraft

  • Published:
Dynamics and Control

Abstract

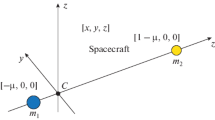
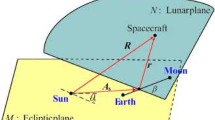
Minimum fuel trajectories from a low Earth parking orbit to a low Moon orbit are obtained for a low-thrust power-limited spacecraft with thrust acceleration levels of the order of 10−3 G. The trajectories are found by matching an Earth spiral to a Moon spiral at some intermediate distance. Results are given for the planar case and for the three dimensional case where the Moon orbit is polar.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Abbreviations

H :

Hamiltonian function

P :

power

U :

gravity potential

M :

Jacobian matrix

a :

thrust acceleration

h :

angular momentum

i :

inclination angle

m :

mass of the spacecraft

n :

angular rate of the Earth-Moon system

r :

radius

t :

time

v :

velocity

π:

angular coordinate in the orbit plane

λ:

adjoint variable (Lagrange multiplier)

μ e , μ m :

gravity coefficient of Earth, Moon

σ:

state

ω:

right ascension of the node

\([\overrightarrow ]\),\(\widehat{[ ]}\) :

vector and a unit vector

[]o, []f :

variable evaluated at initial, final time

[]1, []2:

quantity related to body 1,2 (interchangeably the Earth and the Moon)

References

  1. Golan, O. M., and Breakwell, J. V., “Minimum fuel trajectories for a low-thrust power-limited mission to the moon and to lagrange pointsl 4 andl 5,” inAAS/AIAA Astrodynamics Specialist Conference, stowe, Vermont, August, 1989.

  2. Breakwell, J. V., and Rauch, H. E., “Asymptotic matching in power-limited interplanetary transfers,” inSpace Flight Mechanics Specialist Symposium, AAS Science and Technology Series, Vol. 11, 1967.

  3. Bryson, A. E., Jr., and Ho, Y.-C.,Applied Optimal Control, Hemisphere Publishing Corporation, 1975.

  4. Battin, R. H.,An Introduction to the Mathematics and Methods of Astrodynamics. AIAA Education Series, American Institute of Aeronautics and Astronautics, 1987.

  5. Szebehely, R.,Theory of Orbits, the Restricted Problem of Three Bodies, Academic Press, 1967.

Download references

Author information

Authors and Affiliations

  1. Department of Aeronautics and Astronautics, Stanford University, 94305, Stanford, CA, USA

    Oded M. Golan & John V. Breakwell

Authors
  1. Oded M. Golan
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. John V. Breakwell
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Received his Ph.D. under Professor John V. Breakwell in 1990. Currently at Rafael, MOD, Israel.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Golan, O.M., Breakwell, J.V. Minimum fuel lunar trajectories for a low-thrust power-limited spacecraft. Dynamics and Control 4, 383–394 (1994). https://doi.org/10.1007/BF01974142

Download citation

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF01974142

Keywords

Search

Navigation