Abstract
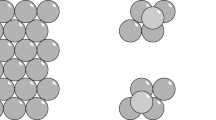
We consider finite packings of unit-balls in Euclidean 3-spaceE 3 where the centres of the balls are the lattice points of a lattice polyhedronP of a given latticeL 3⊃E3. In particular we show that the facets ofP induced by densest sublattices ofL 3 are not too close to the next parallel layers of centres of balls. We further show that the Dirichlet-Voronoi-cells are comparatively small in this direction. The paper was stimulated by the fact that real crystals in general grow slowly in the directions normal to these dense facets.
The results support, to some extent, the hypothesis that real crystals grow preferably such that they need little volume, i.e that they are locally dense.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
U.Betke, P.Gritzmann, J. M.Wills, Slices of L. Fejes Tóth's sausage conjecture,Mathematika 29 (1982) 194–201.MR 84m: 52017
A. H.Boerdijk, Some remarks concerning close-packing of equal spheres,Philips Res. Rep. 7 (1952) 303–313.MR 14310
P.Gritzmann, J. M.Wills, Finite packing and covering,Stud. Sci. Math. Hung. 21 (1986) 149–162.MR 88h: 52022
P. M.Gruber, G. G.Lekkerkerker,Geometry of numbers; North-Holland, Amsterdam, 1987.MR 88j: 11034
W.Kleber,Einführung in die Kristallographie; VEB Verlag Technik Berlin, 1973.
J. M.Wills, On the density of finite packings,Acta. Math. Hung. 46 (1985) 205–210.MR 87e: 52025
Author information
Authors and Affiliations
Additional information
Dedicated to A. Florian on the occasion of this 60th birthday
Rights and permissions
About this article
Cite this article
Wills, J.M. Locally dense finite lattice packings of spheres. Period Math Hung 22, 139–146 (1991). https://doi.org/10.1007/BF01960503
Received:
Issue Date:
DOI: https://doi.org/10.1007/BF01960503