Skip to main content
SpringerLink
Log in

Realization of 2-D denominator-separable digital filter transfer functions using complex arithmetic

  • Published:
Multidimensional Systems and Signal Processing Aims and scope Submit manuscript

Abstract

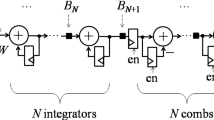
In this paper the problem of realizing 2-D denominator-separable digital filter transfer functions is considered for processing of real sequences. The approach is based on expressing the given 2-D transfer function as a sum of two reduced-order rational transfer functions with complex coefficients. New structures are obtained for equivalent reduced-order, complex-coefficient, 2-D transfer functions. All the realizations are basically parallelform structures with minimum-norm, low round-off noise and freedom from overflow limit cycles. A comparison of the different structures is also made.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • P.A. Regalia, S.K. Mitra and J. Fadavi-Ardekani, “Implementation of real coefficient digital filters using complex arithmetic,”IEEE Trans. on Circuits and Systems, vol. CAS-34, pp. 345–353, 1987.

    Article  Google Scholar 

  • S.G. Tzafestas (ed.), “Multidimensional systems,”Techniques and Applications, Marcel Dekker: New York and Basel, Switzerland, 1986.

    Google Scholar 

  • M.Y. Dabbagh and W.E. Alexander, “Multiprocessor implementation of 2-D denominator separable digital filters for real-time processing,”IEEE Trans. on Acoustics, Speech, and Signal Processing, vol. ASSP-37, pp. 872–881, 1989.

    Google Scholar 

  • D.E. Dudgeon and R.M. Mersereau,Multidimensional Digital Signal Processing, Prentice Hall: Englewood Cliffs, NJ, 1984.

    Google Scholar 

  • N.K. Bose,Applied Multidimensional System Theory, Van Nostrand Reinhold: New York, 1982.

    Google Scholar 

  • K. Mondal, S.K. Mitra and J. Szazupak, “An alternate parallel realization of digital transfer function,”Proc. of the IEEE, vol. 65, pp. 577–578, 1977.

    Google Scholar 

  • D.J. Kuck,The Structure of Computers and Computations, vol.1, Wiley: New York, 1978.

    Google Scholar 

  • A. Weste and K. Eshraghian,Principles of CMOS VLSI Design. A System Perspective, Addison-Wesley: Reading, MA, 1985

    Google Scholar 

  • C.W. Barnes and A.T. Fam, “Minimum norm recursive digital filters that are free of overlow limit cycles,”IEEE Trans. Circuits and Systems, vol. CAS-24, pp. 569–574, 1977.

    Article  Google Scholar 

  • W.L. Mills, C.T. Mullies and R.A. Roberts, “Digial filter realization without overflow oscillations,”IEEE Trans. Acoustics, Speech, and Signal Processing, vol. ASSP-26, pp. 334–338, 1978.

    Google Scholar 

  • D. Lehner, Über Beschreibungen und Realisierungen multidimensionaler Digitalfilter, Ph.D. thesis, University of Erlangen-Nürnberg, F.R. Germany, 1988.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Lehrstuhl für Allgemeine und Theoretische Elektrotechnik, Universität Erlangen-Nürnberg, Cauerstrasse 7, D-8520, Erlangen, F.R. Germany

    D. Raghuramireddy & R. Unbehauen

Authors
  1. D. Raghuramireddy
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. R. Unbehauen
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Raghuramireddy, D., Unbehauen, R. Realization of 2-D denominator-separable digital filter transfer functions using complex arithmetic. Multidim Syst Sign Process 2, 319–336 (1991). https://doi.org/10.1007/BF01952238

Download citation

  • Received:

  • Revised:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF01952238

Keywords

Search

Navigation