Skip to main content
SpringerLink
Log in

On systems of particles with finite-range and/or repulsive interactions

  • Published:
Communications in Mathematical Physics Aims and scope Submit manuscript

Abstract

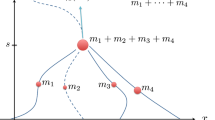
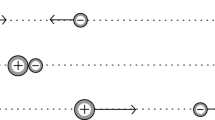
In an arbitrary system of particles with central repulsive interactions, right and left velocities exist at each moment of time, including infinity. An arbitrary system of particles with finite-range interactions splits into independent bounded clusters. The number of collisions in Sinai's billiard is finite.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Sinai, Ya.G.: Billiard trajectories in polyhedral angle. Usp. Mat. Nauk33, 231–232 (1978)

    Google Scholar 

  2. Galperin, G.A.: Elastic collisions of particles on the line. Usp. Mat. Nauk33, 211–212 (1978)

    Google Scholar 

  3. Leontovich, A.M.: On existence of non-bounded oscillating trajectories in a billiard problem. Dokl. Akad. Nauk145, 523–526 (1962)

    Google Scholar 

  4. Sandri, G., Sullivan, R.D., Noren, P.: Collisions of three hard spheres. Phys. Rev. Lett.13, 743–745 (1964)

    Google Scholar 

  5. Hunziker, W.: TheS-matrix in classical mechanics. Commun. Math. Phys.8, 282–299 (1968)

    Google Scholar 

  6. Saari, D.: Expanding gravitational systems. Trans. AMS156, 219–240 (1971)

    Google Scholar 

  7. Moser, J.: The scattering problem for some particle system on the line. In: Lecture notes in mathematics597, 441–463 (1978)

    Google Scholar 

  8. Halpern, B.: Strange billiard tables. Trans. AMS232, 297–306 (1977) See also Mathematical Calendar 79, p. “January”. Berlin, Heidelberg, New York: Springer 1979

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Institut des Hautes Etudes Scientifiques, F-91440, Bures-sur-Yvette, France

    L. N. Vaserstein

Authors
  1. L. N. Vaserstein
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Communicated by D. Ruelle

Rights and permissions

Reprints and permissions

About this article

Cite this article

Vaserstein, L.N. On systems of particles with finite-range and/or repulsive interactions. Commun.Math. Phys. 69, 31–56 (1979). https://doi.org/10.1007/BF01941323

Download citation

  • Received:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF01941323

Keywords

Search

Navigation